题目内容
给出以下四个命题,其中所有正确命题的序号为: .
(1)“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件;
(2)已知线性回归方程
=3+2x,当变量x增加2个单位,其预报值
平均增加4个单位;
(3)函数f(x)=ex-(
)x在区间(-1,1)上只有1个零点;
(4)命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2=0”;
(5)设随机变量ξ服从正态分布N(2,9),若P(ξ>c+1)=P(ξ<c-1),则c等于3.
(1)“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件;
(2)已知线性回归方程
| ∧ |
| y |
| ∧ |
| y |
(3)函数f(x)=ex-(
| 1 |
| 2 |
(4)命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2=0”;
(5)设随机变量ξ服从正态分布N(2,9),若P(ξ>c+1)=P(ξ<c-1),则c等于3.
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1)直接利用充分条件,必要条件的概念判断;
(2)由线性回归方程知,变量x增加2个单位,其预报值平均增加4个单位是正确的;
(3)求导判断函数的单调性,然后由零点存在性定理得答案;
(4)直接写出原命题的逆否命题判断;
(5)由正态分布的概率求法计算c的值,然后判断.
(2)由线性回归方程知,变量x增加2个单位,其预报值平均增加4个单位是正确的;
(3)求导判断函数的单调性,然后由零点存在性定理得答案;
(4)直接写出原命题的逆否命题判断;
(5)由正态分布的概率求法计算c的值,然后判断.
解答:
解:对于(1),由b2=ac,不一定有a、b、c成等比数列,反之,由a、b、c成等比数列,一定有b2=ac,
∴“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件,命(1)正确;
对于(2),线性回归方程为
=3+2x时,当变量x增加2个单位,
其预报值平均增加[3+2(x+2)]-(3+2x)=4个单位,故命题(2)正确;
对于(3),由f(x)=ex-(
)x,得:
f′(x)=ex+(
)x•ln2>0,
∴f(x)在(-1,1)上单调递增,
又f(-1)=
-2<0,f(1)=e-
>0,
∴函数f(x)=ex-(
)x在区间(-1,1)上只有1个零点,命题(3)正确;
对于(4),命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,命题(4)错误;
对于(5),∵随机变量ξ服从正态分布N(2,9),且P(ξ>c+1)=P(ξ<c-1),
则c+1-2=2-c+1,c=2,故命题(5)错误.
∴正确命题的序号是(1)(2)(3).
故答案为:(1)(2)(3).
∴“b2=ac”是“实数a、b、c成等比数列”的必要而不充分条件,命(1)正确;
对于(2),线性回归方程为
| ∧ |
| y |
其预报值平均增加[3+2(x+2)]-(3+2x)=4个单位,故命题(2)正确;
对于(3),由f(x)=ex-(
| 1 |
| 2 |
f′(x)=ex+(
| 1 |
| 2 |
∴f(x)在(-1,1)上单调递增,
又f(-1)=
| 1 |
| e |
| 1 |
| 2 |
∴函数f(x)=ex-(
| 1 |
| 2 |
对于(4),命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,命题(4)错误;
对于(5),∵随机变量ξ服从正态分布N(2,9),且P(ξ>c+1)=P(ξ<c-1),
则c+1-2=2-c+1,c=2,故命题(5)错误.
∴正确命题的序号是(1)(2)(3).
故答案为:(1)(2)(3).
点评:本题考查命题的真假判断与应用,考查了函数零点的判断方法,训练了正态分布概率的求法,是中档题.

练习册系列答案
相关题目
设定义在(0,
)上的函数y=2sinx的图象分别与y=cosx,y=tanx的图象交于点(x1,y1),(x2,y2),则
y1+y2=( )
| π |
| 2 |
| 5 |
A、3+
| ||
B、2+
| ||
C、3+
| ||
D、2+
|
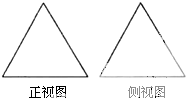 如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )
如图是两个全等的正三角形,给定下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中真命题的个数是( )| A、3 | B、2 | C、1 | D、0 |
设全集U=R,A={x∈N|y=ln(2-x)},B={x|2x(x-2)≤1},A∩B=( )
| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{1} |
| D、{0,1} |
