Question

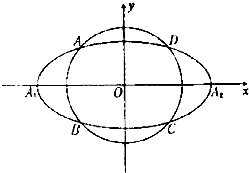如图，动圆C₁：x²+y²=t²，1＜t＜3，与椭圆C₂：

x2

a2

+

y2

b2

=1相交于A，B，C，D四点，点A₁，A₂分别为C₂的左，右顶点．椭圆C₂的一个焦点为（2

2

，0），离心率为

2 2

3

．
（1）求椭圆C₂的方程；   
（2）当t为何值时，矩形ABCD的面积取得最大值？并求出其最大面积；
（3）求直线AA₁与直线A₂B交点M的轨迹方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知条件得

c=2 2 c a = 2 2 3

，由此能求出椭圆C₂的方程．
（2）设A（x₀，y₀），则矩形ABCD的面积S+4|x₀y₀|，x02y02=x02(1-

x02

9

)，由此能求出矩形ABCD的面积的最大值及相应的t的值．
（3）设A（x₀，y₀），B（x₀，-y₀），A₁（-3，0），A₂（3，0），则y2=

-y02

x02-9

(x2-9)，y02=1-

x02

9

，由此能求了出M的轨迹方程．

解答： 解：（1）∵椭圆C₂：

x2

a2

+

y2

b2

=1的一个焦点为（2

2

，0），
离心率为

2 2

3

，
∴

c=2 2 c a = 2 2 3

，解得a=3，∴b²=9-8=1，
∴椭圆C₂的方程

x2

9

+y2=1．…（4分）
（2）设A（x₀，y₀），则矩形ABCD的面积S+4|x₀y₀|，…（1分）
由

x02

9

+y02=1，得y02=1-

x02

9

，
∴x02y02=x02(1-

x02

9

)=-

1

9

（x02-

9

2

）²+

9

4

，
∴x02=

9

2

时，(x02y02)max=

9

4

，
∴Smax=4×

3

2

=6，
此时t=

x02+y02

=

x02+(1- x02 9 )

=

5

．
（3）设A（x₀，y₀），B（x₀，-y₀），A₁（-3，0），A₂（3，0），
直线AA₁的方程为y=

y0

x0+3

(x+3)，①
直线A₂B的方程为y=

-y0

x0-3

(x-3)，②
由①②得y2=

-y02

x02-9

(x2-9)，③
又点A（x₀，y₀）在椭圆上，故y02=1-

x02

9

，④
把④代入③，得

x2

9

-y2=1，
∴M的轨迹方程为

x2

9

-y2=1，x＜-3，y＜0．

点评：本题考查椭圆方程的求法，考查矩形面积的最大值的求法，考查点的轨迹方程的求法，解题时要认真审题，注意函数与方程思想的合理运用．