题目内容
20．在△ABC中，若sinAcosB=1一cosAsinB，则这个三角形是直角三角形．分析 移项后，利用两角和的正弦公式即可得出sinC=1，于是C=$\frac{π}{2}$．
解答 解：∵sinAcosB=1一cosAsinB，∴sinAcosB+cosAsinB=1，即sin（A+B）=sinC=1，
∴C=$\frac{π}{2}$．
∴△ABC是直角三角形．
故答案为：直角．
点评 本题考查了两角和的正弦公式，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10．已知实数x，y满足$\left\{\begin{array}{l}{5x+2y-18≤0}\\{2x-y≥0}\\{x+y-3≥0}\end{array}\right.$，若直线kx-y+1=0经过该可行域，则实数k的最大值是（ ）
| A． | 1 | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |
5．已知集合A={x|x=2k+1，k∈Z}，集合B={x|x=4k±1，k∈Z}，则（ ）
| A． | A⊆B | B． | A?B | C． | A=B | D． | B⊆A |
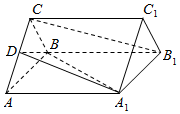如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是$\sqrt{3}$，D是AC的中点．