题目内容
10.已知实数x,y满足$\left\{\begin{array}{l}{5x+2y-18≤0}\\{2x-y≥0}\\{x+y-3≥0}\end{array}\right.$,若直线kx-y+1=0经过该可行域,则实数k的最大值是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 先根据约束条件画出可行域,再利用直线kx-y+2=0过定点(0,1),再利用k的几何意义,只需求出直线kx-y+1=0过点B(2,4)时,k值即可.
解答 解:直线kx-y+2=0过定点(0,1),
作可行域如图所示,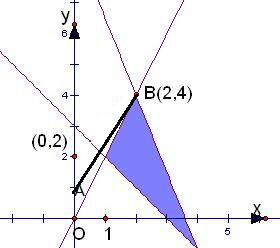 ,
,
由$\left\{\begin{array}{l}{5x+2y-18=0}\\{2x-y=0}\end{array}\right.$,得B(2,4).
当定点(0,1)和B点连接时,斜率最大,此时k=$\frac{4-1}{2-0}$=$\frac{3}{2}$,
则k的最大值为:$\frac{3}{2}$
故选:B.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.命题p:若$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,4),则$\overrightarrow{a}$∥$\overrightarrow{b}$;命题q:若$\overrightarrow{a}$=(1,-3),$\overrightarrow{b}$=(4,-2),λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直,则λ=1,则下列命题中真命题是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
15.已知复数z=$\frac{5i}{2+i}$-3i,则|z|等于( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |