题目内容
14.求函数f(x)=3sin2x+8cos2x-4,x∈[0,$\frac{π}{2}$]的值域.分析 由题意和辅助角公式可得f(x)=5sin(2x+φ),φ=arctan$\frac{4}{3}$,由x∈[0,$\frac{π}{2}$]可得2x+φ∈[arctan$\frac{4}{3}$,π+arctan$\frac{4}{3}$],由正弦函数值域可得.
解答 解:由三角函数公式化简可得f(x)=3sin2x+8cos2x-4
=3sin2x+4(2cos2x-1)=3sin2x+4cos2x=5sin(2x+φ),
其中tanφ=$\frac{4}{3}$,故φ=arctan$\frac{4}{3}$,
∵x∈[0,$\frac{π}{2}$],∴2x∈[0,π],∴2x+φ∈[arctan$\frac{4}{3}$,π+arctan$\frac{4}{3}$],
∴当2x+φ=$\frac{π}{2}$时,f(x)=5sin(2x+φ)取最大值5;
当2x+φ=π+arctan$\frac{4}{3}$时,f(x)=5sin(2x+φ)取最小值5×(-$\frac{4}{5}$)=-4.
故函数的值域为[-4,5].
点评 本题考查三角函数求最值,涉及辅助角公式和同角三角函数基本关系,属中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
9.在三角形ABC中,角A、B、C的对边分别为a,b,c,且满足$\frac{a}{6}$=$\frac{b}{4}$=$\frac{c}{3}$,则$\frac{sin2A}{sinB+sinC}$=( )
| A. | -$\frac{11}{14}$ | B. | $\frac{12}{7}$ | C. | -$\frac{11}{24}$ | D. | -$\frac{7}{12}$ |
6.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个向量,则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
5.函数$f(x)=\sqrt{x+1}-\frac{x}{2-x}$的定义域为( )
| A. | {x|x≥-1} | B. | {x|x≠2} | C. | [-1,2)∪(2,+∞) | D. | (-1,2) |
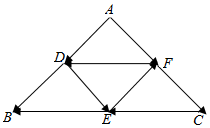 如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.
如图,D,E,F分别是等腰直角三角形ABC各边的中点,∠BAC=90°.