题目内容
2．
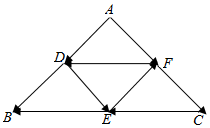如图，D，E，F分别是等腰直角三角形ABC各边的中点，∠BAC=90°．①写出图中与$\overrightarrow{DE}$，$\overrightarrow{FD}$长度相等的向量；
②分别写出图中与向量$\overrightarrow{DE}$，$\overrightarrow{FD}$共线的向量．
分析 ①根据题意△ABC是等腰直角三角形，写出与图中$\overrightarrow{DE}$、$\overrightarrow{FD}$长度相等的向量即可；
②写出图中与向量$\overrightarrow{DE}$、$\overrightarrow{FD}$共线的向量即可．
解答 解：①根据题意，△ABC是等腰直角三角形，
所以图中与$\overrightarrow{DE}$长度相等的向量是$\overrightarrow{AD}$，$\overrightarrow{DB}$，$\overrightarrow{AF}$，$\overrightarrow{FC}$和$\overrightarrow{DF}$；
和向量$\overrightarrow{FD}$长度相等的向量是$\overrightarrow{CE}$和$\overrightarrow{EB}$；
②图中与向量$\overrightarrow{DE}$共线的向量是$\overrightarrow{AF}$和$\overrightarrow{FC}$；
与向量$\overrightarrow{FD}$共线的向量是$\overrightarrow{CE}$和$\overrightarrow{EB}$．
点评 本题考查了平面向量的模长与共线的应用问题，是基础题目．
练习册系列答案
英才计划同步课时高效训练系列答案
相关题目
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，顶点分别为A1，A2，B1，B2，左右焦点分别为F1，F2，延长B1F2与A2B2交于P点，若∠B1PA2为钝角，则此椭圆的离心率的取值范围为$（\frac{{\sqrt{5}-1}}{2}，1）$．
如图，矩形ABCD中AD边的长为1，AB边的长为2，矩形ABCD位于第一象限，且顶点A，D分别在x轴y轴的正半轴上（含原点）滑动，则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是（ ）