题目内容
6.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个向量,则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的( )| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 $\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个向量,则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$?λ=μ=v?λ2+μ2+v2=0,即可判断出结论.
解答 解:∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$,$\overrightarrow{{e}_{3}}$是不共面的三个向量,则λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$?λ=μ=v?λ2+μ2+v2=0,
∴λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$+v$\overrightarrow{{e}_{3}}$=$\overrightarrow{0}$是λ2+μ2+v2=0的充要条件,
故选:C.
点评 本题考查了空间向量基本定理、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11. 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )
 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别在x轴y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}$$•\overrightarrow{OC}$的最大值是( )| A. | $\sqrt{5}$ | B. | 5 | C. | 6 | D. | 7 |
17.设函数$f(x)={2^{\sqrt{-{x^2}+2x+\frac{5}{4}}}}$,对于给定的正数K,定义函数fg(x)=$\left\{{\begin{array}{l}{f(x),f(x)≥K}\\{K,f(x)<K}\end{array}}$,若对于函数$f(x)={2^{\sqrt{-{x^2}+2x+\frac{5}{4}}}}$定义域内的任意x,恒有fg(x)=f(x),则( )
| A. | K的最小值为1 | B. | K的最大值为1 | C. | K的最小值为$2\sqrt{2}$ | D. | K的最大值为$2\sqrt{2}$ |
18.若一段圆弧的长度等于该圆内接正三角形的边长,则这段弧所对圆心角弧度为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
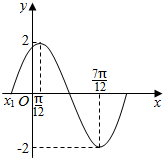 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.