题目内容
已知圆锥曲线C的焦点F1,F2在x轴上,离心率为
,其上的动点P满足|PF1|+|PF2|=4,
(Ⅰ)求曲线C的标准方程;
(Ⅱ)若曲线C的一条切线l交x、y轴正半轴交于A,B两点,求S△AOB的最小值和此时直线l的方程.
| ||
| 2 |
(Ⅰ)求曲线C的标准方程;
(Ⅱ)若曲线C的一条切线l交x、y轴正半轴交于A,B两点,求S△AOB的最小值和此时直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆的定义求出a,利用离心率为
,求出c,即可求出b,从而可求曲线C的标准方程;
(Ⅱ)方程为y=kx+b(k<0,b>0)与椭圆方程联立,利用△=0,可得b2=4k2+1,表示出S△AOB,利用基本不等式求最小值,从而得到此时直线l的方程.
| ||
| 2 |
(Ⅱ)方程为y=kx+b(k<0,b>0)与椭圆方程联立,利用△=0,可得b2=4k2+1,表示出S△AOB,利用基本不等式求最小值,从而得到此时直线l的方程.
解答:
解:(Ⅰ)∵动点P满足|PF1|+|PF2|=4,
∴2a=4,
∴a=2,
∵离心率为
,
∴
=
,
∴c=
,
∴b=
=1,
∴曲线C的标准方程为
+y2=1(3分)
(Ⅱ)由已知直线l的斜率存在且不为0,l交x、y轴正半轴交于A、B两点,
可设方程为y=kx+b(k<0,b>0)(4分)
由
消去y得(4k2+1)x2+8kbx+4b2-4=0(6分)
△=64k2b2-4(4k2+1)(4b2-4)=0,∴b2=4k2+1(8分)
∴S△AOB=
|-
||b|=
|4k+
|=|2k|+|
|≥2(9分)
当且仅当|2k|=|
|(k<0)即k=-
时等号成立,此时b=
(11分)
直线l的方程y=-
x+
,△AOB面积的最小值为2.(12分)
∴2a=4,
∴a=2,
∵离心率为
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
∴c=
| 3 |
∴b=
| a2-c2 |
∴曲线C的标准方程为
| x2 |
| 4 |
(Ⅱ)由已知直线l的斜率存在且不为0,l交x、y轴正半轴交于A、B两点,
可设方程为y=kx+b(k<0,b>0)(4分)
由
|
△=64k2b2-4(4k2+1)(4b2-4)=0,∴b2=4k2+1(8分)
∴S△AOB=
| 1 |
| 2 |
| b |
| k |
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| 2k |
当且仅当|2k|=|
| 1 |
| 2k |
| 1 |
| 2 |
| 2 |
直线l的方程y=-
| 1 |
| 2 |
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
给出以下四个命题:
①“全等的三角形面积相等”;
②“对角线互相垂直且相等的四边形是正方形”;
③“若x2≠9,则x≠3”;
④“若x2>y2,则x>y”的否命题.
其中真命题是( )
①“全等的三角形面积相等”;
②“对角线互相垂直且相等的四边形是正方形”;
③“若x2≠9,则x≠3”;
④“若x2>y2,则x>y”的否命题.
其中真命题是( )
| A、①③ | B、②③ | C、①② | D、①④ |
若x,y满足约束条件
,则z=2x+3y的最小值为( )
|
| A、7 | B、10 | C、16 | D、19 |
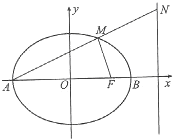 如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且
如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且