题目内容
1.某中学用校车接送教师上下班,从起点站出发后包括终点站一共停4个站,若在起点站上了5个人,中途没有人上车,每位老师在每个站下车的概率相等.若某站没有人下车,则校车就不停,车在终点站一定会停,起点站不算停车.(1)求校车除终点站外只停一次的概率;
(2)设校车停车次数为ξ,求ξ的分布列和期望.
分析 (1)设“校车除终点站外只停一次”为事件A,可得P(A)=$\frac{3({2}^{5}-{∁}_{5}^{0})}{{4}^{5}}$.
(2)由题意可得ξ=1,2,3,4.P(ξ=1)=$\frac{{∁}_{5}^{5}}{{4}^{5}}$,P(ξ=2)=$\frac{93}{1024}$,P(ξ=4)=$\frac{M}{{4}^{5}}$,其中M=${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{1}$+3${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{2}$+3${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{3}$+3${∁}_{5}^{1}{∁}_{4}^{2}{∁}_{2}^{2}$=390,P(ξ=3)=1-P(ξ=1)-P(ξ=2)-P(ξ=4).
解答 解:(1)设“校车除终点站外只停一次”为事件A,则P(A)=$\frac{3({2}^{5}-{∁}_{5}^{0})}{{4}^{5}}$=$\frac{93}{1024}$.
(2)由题意可得ξ=1,2,3,4.
P(ξ=1)=$\frac{{∁}_{5}^{5}}{{4}^{5}}$=$\frac{1}{1024}$,P(ξ=2)=$\frac{93}{1024}$,
P(ξ=4)=$\frac{M}{{4}^{5}}$,其中M=${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{1}$+3${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{2}$+3${∁}_{5}^{1}{∁}_{4}^{1}{∁}_{3}^{3}$+3${∁}_{5}^{1}{∁}_{4}^{2}{∁}_{2}^{2}$=390,∴P(ξ=4)=$\frac{390}{1024}$,
∴P(ξ=3)=1-P(ξ=1)-P(ξ=2)-P(ξ=4)=$\frac{540}{1024}$.
可得ξ的分布列:
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{1024}$ | $\frac{93}{1024}$ | $\frac{540}{1024}$ | $\frac{390}{1024}$ |
点评 本题考查了古典概率计算公式、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.

| A. | 有最大值 | B. | 是减函数 | C. | 是增函数 | D. | 有最小值 |
| A. | -1 | B. | -e | C. | 1 | D. | e |
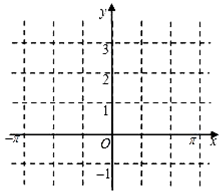 已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心,
已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.