题目内容
若函数f(x)=loga(x2+
x),(a>0,a≠1)在区间(
,+∞)内恒有f(x)<0,则f(x)的单调递减区间是( )
| 3 |
| 2 |
| 1 |
| 2 |
A、(-∞,-
| ||
B、(-∞,-
| ||
C、(-
| ||
| D、(0,+∞) |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:求出函数x2+
x在在区间(
,+∞)内的范围,利用函数在区间(
,+∞)内恒有f(x)<0,即可求出a的范围,然后求解函数的单调减区间.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:x∈(
,+∞)时,x2+
x=(x+
)2-
>1,
函数f(x)=loga(x2+
x)(a>0且a≠1)在区间(
,+∞)内恒有f(x)<0,
所以a∈(0,1),
∴函数的f(x)的定义域为x2+
x>0,解得x<-
,或x>0,
由复合函数的单调性可知f(x)的单调递减区间:(-∞,-
).
故选:B.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 16 |
函数f(x)=loga(x2+
| 3 |
| 2 |
| 1 |
| 2 |
所以a∈(0,1),
∴函数的f(x)的定义域为x2+
| 3 |
| 2 |
| 3 |
| 2 |
由复合函数的单调性可知f(x)的单调递减区间:(-∞,-
| 3 |
| 2 |
故选:B.
点评:本题考查复合函数的单调性以及二次函数、对数函数的单调性的应用,考查计算能力

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
若a,b均为正实数,且
+
=1,则a+b的最小值是( )
| 4 |
| a |
| 3 |
| b |
A、6+2
| ||
B、7+2
| ||
C、6+4
| ||
D、7+4
|
已知函数f(x)=
,则f(2-log
3)=( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合P={x|0≤x≤4},M={y|0≤y≤2},则下列表示P到M的映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
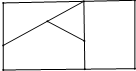 如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有
如图,用6种不同的颜色为一块广告牌着色,要求在四个区域中相邻的区域不用同一种颜色,则共有