题目内容
12．已知集合A={x||x-1|＜1}，B={x|1-$\frac{1}{x}$≥0}，则A∩B=（ ）| A． | {x|1≤x＜2} | B． | {x|0＜x＜2} | C． | {x|0＜x≤1} | D． | {x|0＜x＜1} |
分析 求出A，B中不等式的解集，找出A与B的交集即可．
解答 解：由|x-1|＜1，即-1＜x-1＜1，即0＜x＜2，即A={x|0＜x＜2}，
由1-$\frac{1}{x}$≥0，即$\frac{x-1}{x}$≥0，解得x≥1或x＜0，即B={x|x≥1或x＜0}
则A∩B={x|1≤x＜2}，
故选：A
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3．汉中最美油菜花节期间，5名游客到四个不同景点游览，每个景点至少有一人，则不同的游览方法共有（ ）种．
| A． | 120 | B． | 625 | C． | 240 | D． | 1024 |
20．已知复数z满足$\frac{z}{|z|}=\frac{3}{5}+\frac{4}{5}i$，则z的实部与虚部之比为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $-\frac{4}{3}$ | D． | $-\frac{3}{4}$ |
4．已知等差数列{an}的公差不为0，a1=1，且a1，a2，a4成等比数列，设{an}的前n项和为Sn，则Sn=（ ）
| A． | $\frac{（n+1）^{2}}{4}$ | B． | $\frac{n（n+3）}{4}$ | C． | $\frac{n（n+1）}{2}$ | D． | $\frac{{n}^{2}+1}{2}$ |
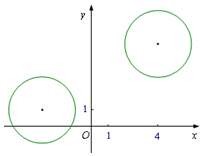在平面直角坐标系xOy中，已知圆${C_1}：{（x+3）^2}+{（y-1）^2}=4$和圆${C_2}：{（x-4）^2}+{（y-5）^2}=4$．