题目内容
已知数列{an}满足,a1=1,an>0且an+12=
(n∈N*)
(1)求数列{an}的通项公式;
(2)数列{bn}的前n项和Sn满足:b1=1,
=
+16n2-8n-3,求数列{2nbn}的前n项和An.
(3)记Tn=a12+a22+…+an2,若T2n+1-Tn≤
对任意n∈N*恒成立,求正整数m的最小值.
| an2 |
| 4an2+1 |
(1)求数列{an}的通项公式;
(2)数列{bn}的前n项和Sn满足:b1=1,
| Sn+1 |
| an2 |
| Sn |
| an+12 |
(3)记Tn=a12+a22+…+an2,若T2n+1-Tn≤
| m |
| 30 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由an+12=
(n∈N*),得
=
+4,由此能求出an=
.
(2)由已知条件推导出an+12Sn+1=an2Sn+1,从而得到Sn=n(4n-3),进而得到bn=8n-7,由此利用裂项求和法能求出数列{2nbn}的前n项和An.
(3)设Bn=T2n+1-Tn,则Bn+1-Bn=
+
-
,由此利用已知条件能求出m的最小值.
| an2 |
| 4an2+1 |
| 1 |
| an+12 |
| 1 |
| an2 |
| 1 | ||
|
(2)由已知条件推导出an+12Sn+1=an2Sn+1,从而得到Sn=n(4n-3),进而得到bn=8n-7,由此利用裂项求和法能求出数列{2nbn}的前n项和An.
(3)设Bn=T2n+1-Tn,则Bn+1-Bn=
| 1 |
| 8n+9 |
| 1 |
| 8n+5 |
| 1 |
| 4n+1 |
解答:
(本题满分13分)
解:(1)由an+12=
(n∈N*),
得
=
+4
∵a1=1,an>0,∴
=1,
∴数列{
}是首项为1,公差为4的等差数列,
∴
=1+(n-1)×4=4n-3,
∴an=
.…(3分)
(2)∵b1=1,
=
+16n2-8n-3,
an2=
,an+12=
,
∴16n2-8n-3=(4n-3)(4n+1)=
,
∴an+12Sn+1=an2Sn+1,
∴an2Sn=n,∴Sn=n(4n-3),
∴bn=Sn-Sn-1=[n(4n-3)]-[(n-1)(4n-7)]=8n-7,
当n=1时,8n-7=1=b1,
∴bn=8n-7…(6分)
∵数列{2nbn}的前n项和An,
∴An=2+9•22+17•23+…+(8n-7)•2n,①
2An=22+9•23+17•24+…+(8n-7)•2n+1,②
①-②,得:-An=2+8•22+8•23+…+8•2n-(8n-7)•2n+1
=2+8×
-(8n-7)•2n+1,
∴An=(8n-15)2n+1+30.…(9分)
(3)设Bn=T2n+1-Tn,所以Bn+1-Bn=
+
-
所以Bn+1-Bn=
+
-
<0
所以Bn+1<Bn所以Bn最大值为B1=a22+a32=
所以
≥
,又m是正整数,所以m≥10,
所以m的最小值为10.…(13分)
解:(1)由an+12=
| an2 |
| 4an2+1 |
得
| 1 |
| an+12 |
| 1 |
| an2 |
∵a1=1,an>0,∴
| 1 |
| a12 |
∴数列{
| 1 |
| an2 |
∴
| 1 |
| an2 |
∴an=
| 1 | ||
|
(2)∵b1=1,
| Sn+1 |
| an2 |
| Sn |
| an+12 |
an2=
| 1 |
| 4n-3 |
| 1 |
| 4n+1 |
∴16n2-8n-3=(4n-3)(4n+1)=
| 1 |
| an2an+12 |
∴an+12Sn+1=an2Sn+1,
∴an2Sn=n,∴Sn=n(4n-3),
∴bn=Sn-Sn-1=[n(4n-3)]-[(n-1)(4n-7)]=8n-7,
当n=1时,8n-7=1=b1,
∴bn=8n-7…(6分)
∵数列{2nbn}的前n项和An,
∴An=2+9•22+17•23+…+(8n-7)•2n,①
2An=22+9•23+17•24+…+(8n-7)•2n+1,②
①-②,得:-An=2+8•22+8•23+…+8•2n-(8n-7)•2n+1
=2+8×
| 4(1-2n-1) |
| 1-2 |
∴An=(8n-15)2n+1+30.…(9分)
(3)设Bn=T2n+1-Tn,所以Bn+1-Bn=
| 1 |
| 8n+9 |
| 1 |
| 8n+5 |
| 1 |
| 4n+1 |
所以Bn+1-Bn=
| 1 |
| 8n+9 |
| 1 |
| 8n+5 |
| 2 |
| 8n+2 |
所以Bn+1<Bn所以Bn最大值为B1=a22+a32=
| 14 |
| 45 |
所以
| m |
| 30 |
| 14 |
| 45 |
所以m的最小值为10.…(13分)
点评:本题考查数列的通项公式的求法,考查数列前n项和的求法,考查实数的最小值的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
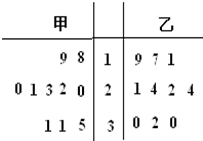 甲、乙两人在10天中每天加工的零件的个数用茎叶图表示如图.中间一列的数字表示零件个数的十位数,两边的数字零件个数的个位数,则这10天中甲、乙两人日加工零件的平均水平
甲、乙两人在10天中每天加工的零件的个数用茎叶图表示如图.中间一列的数字表示零件个数的十位数,两边的数字零件个数的个位数,则这10天中甲、乙两人日加工零件的平均水平