题目内容
已知函数f(x)=x+
-lnx,试判断函数分别在下列条件下的单调性:
(1)a<-1;
(2)a<0;
(3)a∈R.
| a |
| x |
(1)a<-1;
(2)a<0;
(3)a∈R.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:首先,求导数,然后,将导数表达式进行化简,最后,结合二次函数和一元二次不等式对a的取值情况进行分类讨论.
解答:
解:∵f(x)=x+
-lnx,定义域为(0,+∞),
∴f′(x)=1-
-
=
,
(1)令f′(x)>0,x2-x-a>0,
∵方程x2-x-a=0的判别式:
△=1+4a,
∵a<-1,
∴△=1+4a<0,
∴f′(x)>0恒成立,
增区间为:(0,+∞),
此时没有减区间.
(2)当a<0时,
结合(1),此时,△=1+4a<0,
∴f′(x)>0恒成立,
增区间为:(0,+∞),
此时没有减区间.
(3)结合(1),
令f′(x)>0,x2-x-a>0,
∵方程x2-x-a=0的判别式:
△=1+4a,
当△<0时,即a<-
,
此时,只有增区间为:(0,+∞),
此时没有减区间.
当△≥0时,即a≥-
,
此时,增区间为:(
,+∞),
减区间:(0,
).
| a |
| x |
∴f′(x)=1-
| a |
| x2 |
| 1 |
| x |
| x2-x-a |
| x2 |
(1)令f′(x)>0,x2-x-a>0,
∵方程x2-x-a=0的判别式:
△=1+4a,
∵a<-1,
∴△=1+4a<0,
∴f′(x)>0恒成立,
增区间为:(0,+∞),
此时没有减区间.
(2)当a<0时,
结合(1),此时,△=1+4a<0,
∴f′(x)>0恒成立,
增区间为:(0,+∞),
此时没有减区间.
(3)结合(1),
令f′(x)>0,x2-x-a>0,
∵方程x2-x-a=0的判别式:
△=1+4a,
当△<0时,即a<-
| 1 |
| 4 |
此时,只有增区间为:(0,+∞),
此时没有减区间.
当△≥0时,即a≥-
| 1 |
| 4 |
此时,增区间为:(
1+
| ||
| 2 |
减区间:(0,
1+
| ||
| 2 |
点评:本题重点考查了函数的单调区间的求解方法、函数的单调性与导数等知识,属于中档题,重点考查分类讨论思想.

练习册系列答案
相关题目
如图,AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,则
=( )
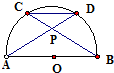
| CD |
| AB |

| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
已知命题p:函数y=x3为R上的奇函数;命题q:若b2=ac,则a,b,c一定成等比数列.下列说法正确的是( )
| A、p或q为假 |
| B、p且q为真 |
| C、¬p且q为真 |
| D、¬p或q为假 |
“0<k<2”是“
+
=1表示椭圆”的( )
| x2 |
| 2 |
| y2 |
| k |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
