题目内容
若直线mx+ny=1经过点（1，2），其中m＞0，n＞0，则log3（2m+n）-log3（mn）的最小值为 ．
考点：对数的运算性质,基本不等式
专题：直线与圆
分析：由已知得m+2n=1，log3（2m+n）-log3（mn）=log3
=log3
=log3（
+
+5），由此利用均值定理能求出log3（2m+n）-log3（mn）的最小值．
| 2m+n |
| mn |
| (m+2n)(2m+n) |
| mn |
| 2m |
| n |
| 2n |
| m |
解答：
解：∵直线mx+ny=1经过点（1，2），
∴m+2n=1，
∵m＞0，n＞0，
∴log3（2m+n）-log3（mn）=log3
=log3
=log3（
+
+5）
≥log3(2
+5)
=log39=2．
当且仅当
=
，即m=n=
时，取“=”，
∴log3（2m+n）-log3（mn）的最小值为2．
故答案为：2．
∴m+2n=1，
∵m＞0，n＞0，
∴log3（2m+n）-log3（mn）=log3
| 2m+n |
| mn |
=log3
| (m+2n)(2m+n) |
| mn |
=log3（
| 2m |
| n |
| 2n |
| m |
≥log3(2
|
=log39=2．
当且仅当
| 2m |
| n |
| 2n |
| m |
| 1 |
| 3 |
∴log3（2m+n）-log3（mn）的最小值为2．
故答案为：2．
点评：本题考查代数式的最小值的求法，是基础题，解题时要注意均值定理的合理运用．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
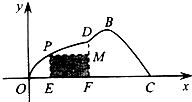如图，某小区为美化环境，准备在小区内草坪的一侧修建一条直路OC；另一侧修建一条休闲大道，它的前一段OD是函数y=k已知一个几何体的三视图是三个全等的边长为l的正方形，如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=3cos2