Question

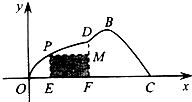如图，某小区为美化环境，准备在小区内草坪的一侧修建一条直路OC；另一侧修建一条休闲大道，它的前一段OD是函数y=k

x

（k＞0）的一部分，后一段DBC是函数y=Asin（ωx+φ）（A＞0，|φ|＜

π

2

），x∈[4，8]时的图象，图象的最高点为B（5，

8

3

3

），DF⊥OC，垂足为F
（Ⅰ）求函数y=Asin（ωx+φ）的解析式和D点坐标；
（Ⅱ）若在草坪内修建如图的儿童游乐园PMFE，问点P落在曲线OD上何处时，儿童乐园的面积最大？

Answer 1

考点：函数模型的选择与应用,函数解析式的求解及常用方法,函数的最值及其几何意义

专题：函数的性质及应用

分析：（Ⅰ）由图易知，A=

8

3

3

，T=

2π

ω

=12⇒ω=

π

6

，又5×

π

6

+Φ=2kπ+

π

2

（k∈Z）⇒Φ=2kπ-

π

3

（k∈Z），又|Φ|＜

π

2

，可求得Φ=-

π

3

，于是可得函数y=Asin（ωx+Φ）的解析式；
（Ⅱ）在y=

8

3

3

sin（

π

6

x-

π

3

）中，令x=4，可得D（4，4），曲线OD的方程为y²=4x（0≤x≤4），设点P（

t2

4

，t）（0≤t≤4），则矩形PMFE的面积为S=（4-

t2

4

）t（0≤t≤4），利用导数可求得儿童乐园的面积的最大值．

解答： 解：（Ⅰ）由图知，A=

8

3

3

，

T

4

=8-5=3，T=

2π

ω

=12，解得ω=

π

6

，…3分
又5×

π

6

+Φ=2kπ+

π

2

（k∈Z），
所以，Φ=2kπ-

π

3

（k∈Z），…4分
又|Φ|＜

π

2

），故Φ=-

π

3

…5分
故y=

8

3

3

sin（

π

6

x-

π

3

）…6分
（Ⅱ）在y=

8

3

3

sin（

π

6

x-

π

3

）中，令x=4，得D（4，4）…7分
从而得曲线OD的方程为y²=4x（0≤x≤4）…8分
设点P（

t2

4

，t），（0≤t≤4），则矩形PMFE的面积为S=（4-

t2

4

）t（0≤t≤4），…9分
因为S′=4-

3t2

4

，由S′=0，得t=

4

3

3

，
当t∈（0，

4

3

3

）时，S′＞0，S递增；当t∈（

4

3

3

，4）时，S′＜0，S递减；
所以当t=

4

3

3

时，S最大，此时点P的坐标为（

4

3

，

4

3

3

）…12分

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查导数的概念及应用，考查转化思想与运算求解能力．