题目内容
9.已知数列{an}满足:a1=1,an=an-12+2an-1(n≥2),若bn=$\frac{1}{{{a_{n+1}}}}+\frac{1}{{{a_n}+2}}$(n∈N*),则数列{bn}的前n项和Sn=1-$\frac{1}{{2}^{{2}^{n}}-1}$.分析 由条件配方,取常用对数,运用等比数列可得an=2${\;}^{{2}^{n-1}}$-1,求出bn=$\frac{1}{{2}^{{2}^{n-1}}-1}$-$\frac{1}{{2}^{{2}^{n}}-1}$,运用数列的求和方法:裂项相消求和,计算即可得到所求和.
解答 解:a1=1,an=an-12+2an-1(n≥2),
即有an+1=an-12+2an-1+1=(an-1+1)2,
两边取常用对数,可得lg(an+1)=lg(an-1+1)2=2lg(an-1+1),
可得lg(an+1)=lg2•2n-1,
可得an=2${\;}^{{2}^{n-1}}$-1,
则bn=$\frac{1}{{{a_{n+1}}}}+\frac{1}{{{a_n}+2}}$=$\frac{1}{{2}^{{2}^{n}}-1}$+$\frac{1}{{2}^{{2}^{n-1}}+1}$=$\frac{1}{({2}^{{2}^{n-1}}-1)({2}^{{2}^{n-1}}+1)}$+$\frac{1}{{2}^{{2}^{n-1}}+1}$
=$\frac{1}{{2}^{{2}^{n-1}}-1}$-$\frac{1}{{2}^{{2}^{n}}-1}$,
则Sn=b1+…+bn═1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{15}$+$\frac{1}{15}$-$\frac{1}{255}$+…+$\frac{1}{{2}^{{2}^{n-1}}-1}$-$\frac{1}{{2}^{{2}^{n}}-1}$
=1-$\frac{1}{{2}^{{2}^{n}}-1}$.
故答案为:1-$\frac{1}{{2}^{{2}^{n}}-1}$.
点评 本题考查数列的通项公式的求法,注意运用取对数,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $(4,6+4\sqrt{2})$ | B. | $(4,6+4\sqrt{2}]$ | C. | $[6+4\sqrt{2},+∞)$ | D. | $(6+4\sqrt{2},+∞)$ |
| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | [-1,3) | B. | [0,3) | C. | [1,3) | D. | (1,3) |
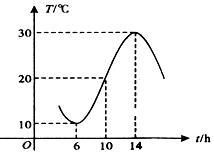 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )| A. | $y=10sin(\frac{π}{8}x+\frac{3π}{4})+20$,x∈[6,14] | B. | $y=10sin(\frac{π}{8}x+\frac{5π}{4})+20$,x∈[6,14] | ||
| C. | $y=10sin(\frac{π}{8}x-\frac{3π}{4})+20$,x∈[6,14] | D. | $y=10sin(\frac{π}{8}x+\frac{5π}{8})+20$,x∈[6,14] |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{5}{18}$ |