题目内容
18.若等差数列{an}的前n项和Sn有最大值,且$\frac{{a}_{11}}{{a}_{10}}$<-1,那么令Sn取最小正值的项数n=( )| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
分析 由题意知,Sn有最大值,所以d<0,因为$\frac{{a}_{11}}{{a}_{10}}$<-1,可得a10>0>a11,且a10+a11<0,再利用求和公式与数列的单调性即可判断出结论.
解答 解:由题意知,Sn有最大值,所以d<0,因为$\frac{{a}_{11}}{{a}_{10}}$<-1,
所以a10>0>a11,且a10+a11<0,
所以S20=10(a1+a20)=10(a10+a11)<0,则S19=19a10>0,
又a1>a2>…>a10>0>a11>a12,所以S10>S9>…>S2>S1>0,S10>S11>…>S19>0>S20>S21,
又S19-S1=a2+a3+…+a19=9(a10+a11)<0,所以S19为最小正值,
故选:C.
点评 本题考查了等差数列的通项公式与求和公式及其单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知圆C1:x2+y2=4,圆C2:x2+y2+6x-8y+16=0,则圆C1和圆C2的位置关系是( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
13.将一颗骰子掷两次,则第二次出现的点数是第一次点数的2倍的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
9.设P为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上且在第一象限内的点,F1,F2分别是双曲线的左、右焦点,PF2⊥F1F2,x轴上有一点A且AP⊥PF1,E是AP的中点,线段EF1与PF2交于点M.若|PM|=2|MF2|,则双曲线的离心率是( )
| A. | 1$+\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 3$+\sqrt{2}$ | D. | 4$+\sqrt{2}$ |
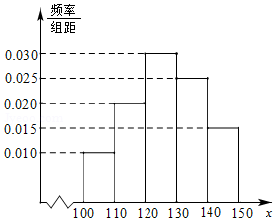 扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.
扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.