题目内容
17.已知O为坐标原点,A,B的坐标分别是(4,0),(0,3),则△AOB外接圆的方程为x2+y2-4x-3y=0.分析 设△AOB的外接圆的方程为:x2+y2+Dx+Ey+F=0,把A(4,0),B(0,3),O(0,0)三点代入能求出圆的方程.
解答 解:设三角形AOB的外接圆的方程为:x2+y2+Dx+Ey+F=0,
把A(4,0),B(0,3),O(0,0)三点代入,得:$\left\{\begin{array}{l}{16+4D+F=0}\\{9+3E+F=0}\\{F=0}\end{array}\right.$,
解得D=-4,E=-3,F=0,
∴三角形AOB外接圆的方程为x2+y2-4x-3y=0.
故答案为:x2+y2-4x-3y=0.
点评 本题考查圆的方程,考查待定系数法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
6. 如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )
如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )
 如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )
如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为( )| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
 如图,在边长为2的正方形中随机撒1000粒豆子,有380粒落到阴影部分,据此估计阴影部分的面积为1.52.
如图,在边长为2的正方形中随机撒1000粒豆子,有380粒落到阴影部分,据此估计阴影部分的面积为1.52.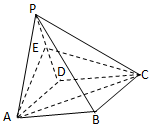 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.