题目内容
12.已知函数f(x)=x-alnx,$g(x)=-\frac{1+a}{x}$.(1)若a=1,求函数f(x)的极值;
(2)设函数h(x)=f(x)-g(x),求函数h(x)的单调区间.
分析 (1)求出函数的导数,解关于导函数的不等式求出函数的单调区间,从而求出函数的极值即可;
(2)求出h(x)的导数,通过讨论a的范围,求出函数的单调区间,从而进一步确定a的范围即可.
解答 解:(1)由题意可知f(x)的定义域为(0,+∞),…(1分)
当a=1时,f(x)=x-lnx,$f'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,…(3分)
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
(2)∵$h(x)=x-alnx+\frac{1+a}{x}$∴$h'(x)=1-\frac{a}{x}-\frac{1+a}{x^2}=\frac{{(x+1)[{x-(1+a)}]}}{x^2}$…(9分)
①当a+1>0即a>-1时,令h'(x)<0得0<x<a+1
令h'(x)>0得x>a+1…(11分)
②当a+1≤0即a≤-1时,h'(x)>0在x∈(0,+∞)上恒成立,…(13分)
综上,当a>-1时,h(x)的递减区间为(0,a+1),递增区间为(a+1,+∞);
当a≤-1时,h(x)的递增区间为(0,+∞),无递减区间. …(14分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
20.已知递增的等比数列{an}中,a1,a2,a3分别为下表中第一、二、三行中某一个数,且a1,a2,a3中的任何两个数不在下表中同一行和同一列,
(1)求数列{an}通项公式;
(2)若数列{bn}满足${b_n}={a_n}+{(-1)^n}ln{a_n}$,若n为偶数,求数列{bn}的前n项和.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(2)若数列{bn}满足${b_n}={a_n}+{(-1)^n}ln{a_n}$,若n为偶数,求数列{bn}的前n项和.
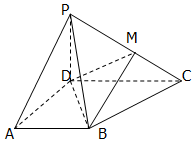 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点. 已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )
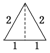
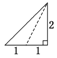
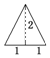
已知an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记S(m,n)表示该数阵中第m行中从左到右的第n个数,则S(8,6)=( )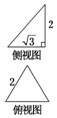 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )