题目内容
7.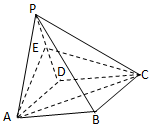 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点.(1)求证:PB∥平面AEC
(2)求证:PB⊥AC.
分析 (1)连接BD交AC于点O,则OE∥PB,由此能证明PB∥平面AEC.
(2)设AD中点为F,连接BF、PF,推导出AC⊥BF,PF⊥AD,从而PF⊥AC,由此能证明AC⊥PB.
解答 证明:(1)连接BD交AC于点O,
∵ABCD是矩形,∴O是BD中点,…(1分)
又∵E是PD中点,
∴OE是△DBP的中位线,
∴OE∥PB,…(2分)
∵OE?平面AEC,PB?平面AEC,…(4分)
∴PB∥平面AEC. …(5分)
(2)设AD中点为F,连接BF、PF.
∵PA=PD=AB=a,
∴AD=BC=$\sqrt{2}a$,AF=$\frac{\sqrt{2}}{2}a$,∴$\frac{AB}{AF}=\frac{BC}{AB}=\sqrt{2}$.
△△ABC∽△FAB,∴AC⊥BF,…(8分)
又PA=PD,F是AD的中点,∴PF⊥AD,…(9分)
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PF?平面PAD,
∴PF⊥面ABCD,…(10分)
∵AC?平面ABCD,∴PF⊥AC,
∵PF∩BF=F,…(11分)
∴AC⊥平面PBF,∵PB?平面ABCD,
∴AC⊥PB.…(12分)
点评 本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
15.“xy≠6”是“x≠2或y≠3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知数列{an}为等差数列,其前n项和为Sn,若a3+a5+a7=$\frac{π}{4}$则sinS9的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |