题目内容
7.已知命题p:?x∈R使得x2+x+1<0;命题q:?x∈[-1,2],使得x2-1>0,则p∧¬q的真假为假.分析 先判断命题p与命题q的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:∵△=1-4=-3<0,
故x2+x+1>0恒成立,
故命题p:?x∈R使得x2+x+1<0为假命题,
当x∈[-1,1]时,x2-1≤0,
故命题q:?x∈[-1,2],使得x2-1>0为假命题,
故p∧¬q为假命题,
故答案为:假
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题,特称命题等知识点,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在直线,点B为该双曲线的焦点,若正方形OABC的边长为2,则a=( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
15.下列是函数y=-(x-3)|x|的递增区间是( )
| A. | (-∞,3) | B. | (0,3) | C. | $({0,\frac{3}{2}})$ | D. | $({\frac{3}{2},3})$ |
16.抛物线x=2y2的准线方程是( )
| A. | y=-$\frac{1}{2}$ | B. | x=-$\frac{1}{8}$ | C. | y=$\frac{1}{2}$ | D. | x=$\frac{1}{8}$ |
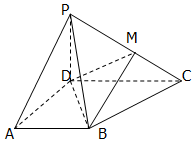 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.