题目内容
（1）在△ABC中，∠B=30°，且a=2
，b=2，解此三角形．
（2）在△ABC中，∠A=45°，∠B=30°，c=10，解此三角形．
| 3 |
（2）在△ABC中，∠A=45°，∠B=30°，c=10，解此三角形．
考点：解三角形
专题：综合题,解三角形
分析：（1）利用正弦定理可得
=
，求出A，分类讨论，即可解此三角形；
（2）先求出C，再利用正弦定理可得
=
=
，即可得出结论．
2
| ||
| sinA |
| 2 |
| sin30° |
（2）先求出C，再利用正弦定理可得
| a |
| sin45° |
| 10 |
| sin105° |
| b |
| sin30° |
解答：
解：（1）∵∠B=30°，且a=2
，b=2，
∴利用正弦定理可得
=
，
∴sinA=
，
∵a＞b，∠B=30°，
∴A=60°或120°，
A=60°时，C=90°，∴c=
=4；
A=1200°时，C=30°，∴c=b=2；
（2）∵∠A=45°，∠B=30°，∴∠C=105°．
∵c=10，
∴利用正弦定理可得
=
=
，
∴a=10
-10，b=5
-5
．
| 3 |
∴利用正弦定理可得
2
| ||
| sinA |
| 2 |
| sin30° |
∴sinA=
| ||
| 2 |
∵a＞b，∠B=30°，
∴A=60°或120°，
A=60°时，C=90°，∴c=
| a2+b2 |
A=1200°时，C=30°，∴c=b=2；
（2）∵∠A=45°，∠B=30°，∴∠C=105°．
∵c=10，
∴利用正弦定理可得
| a |
| sin45° |
| 10 |
| sin105° |
| b |
| sin30° |
∴a=10
| 3 |
| 6 |
| 2 |
点评：本题考查解三角形，着重考查正弦定理的应用，考查分类讨论思想，属于中档题．
练习册系列答案
相关题目
若全集U={1，2，3，4}且∁UA={2}，则集合A的子集共有（ ）
| A、3个 | B、5个 | C、7个 | D、8个 |
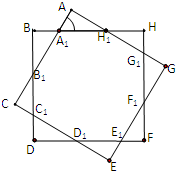如图，制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形．由对称性，图中8个三角形都是全等的三角形，设∠AA1H1=α．