题目内容
已知抛物线C1的焦点F与椭圆C2:x2+
=1的右焦点重合,抛物线的顶点在坐标原点.
(Ⅰ)求这条抛物线C1方程;
(Ⅱ)设圆M过A(1,0),且圆心M在C1的轨迹上,BD是圆M在y轴的截得的弦,当M过去时弦长BD是否为定值?说明理由.
| 4y2 |
| 3 |
(Ⅰ)求这条抛物线C1方程;
(Ⅱ)设圆M过A(1,0),且圆心M在C1的轨迹上,BD是圆M在y轴的截得的弦,当M过去时弦长BD是否为定值?说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆C2:x2+
=1的右焦点求出抛物线C1的焦点为F(
,0),抛物线C1的方程.
(Ⅱ)由已知条件推导出圆的方程为(x-
)2+(y-a)2=(1-
)2+a2,由此能证明弦长|BD|为定值.
| 4y2 |
| 3 |
| 1 |
| 2 |
(Ⅱ)由已知条件推导出圆的方程为(x-
| a2 |
| 2 |
| a2 |
| 2 |
解答:
(Ⅰ)解:∵抛物线C1的焦点与椭圆C2:x2+
=1的右焦点重合,
∴抛物线C1的焦点为F(
,0),
∵抛物线C1的顶点在坐标原点,
∴抛物线C1的方程为y2=2x.
(Ⅱ)证明:∵圆心M在抛物线y2=2x上,
设圆心M(
,a),半径r=
,
圆的方程为(x-
)2+(y-a)2=(1-
)2+a2,
令x=0,得B(0,1+a),D(0,-1+a),
∴|BD|=
=2,
∴弦长|BD|为定值.
| 4y2 |
| 3 |
∴抛物线C1的焦点为F(
| 1 |
| 2 |
∵抛物线C1的顶点在坐标原点,
∴抛物线C1的方程为y2=2x.
(Ⅱ)证明:∵圆心M在抛物线y2=2x上,
设圆心M(
| a2 |
| 2 |
(1-
|
圆的方程为(x-
| a2 |
| 2 |
| a2 |
| 2 |
令x=0,得B(0,1+a),D(0,-1+a),
∴|BD|=
| [(1+a)-(-1+a)]2 |
∴弦长|BD|为定值.
点评:本题考查抛物线方程的求法,考查弦长为定值的证明,解题时要注意圆的简单性质的灵活运用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
某程序框图如图所示,该程序运行后输出的k的值是( )

| A、4 | B、5 | C、6 | D、7 |
下列说法不正确的是( )
| A、方程f(x)=0有实数根?函数y=f(x)有零点 |
| B、函数y=-x2+3x+5有两个零点 |
| C、单调函数至多有一个零点 |
| D、函数f(x)在区间[a,b]上满足f(a)•f(b)<0,则函数f(x)在区间(a,b)内有零点 |
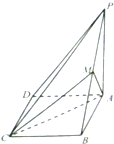 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC= 已知直线l:y=2x与抛物线C:y=
已知直线l:y=2x与抛物线C:y=