题目内容
甲乙两人进行羽毛球比赛，比赛采取五局三胜制，无论哪一方先胜三局则比赛结束，假定甲每局比赛获胜的概率均为
，则甲以3：1的比分获胜的概率为（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：n次独立重复试验中恰好发生k次的概率
专题：计算题,概率与统计
分析：以甲3胜1败而结束比赛，甲只能在1、2、3次中失败1次，第4次胜，即可得出结论．
解答：
解：甲以3：1的比分获胜，甲只能在1、2、3次中失败1次，第4次胜，
因此所求概率为：P=
•(
)3•
=
．
故选：A．
因此所求概率为：P=
| C | 1 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
故选：A．
点评：本题主要考查n次独立重复实验中恰好发生k次的概率，等可能事件的概率，属于基础题．
练习册系列答案
相关题目
在如图所示的程序框图中，当输入x的值为32时，输出x的值为（ ）
| A、1 | B、3 | C、5 | D、7 |
若实数x，y满足：3x+4y-12=0，则x2+y2+2x的最小值是（ ）
| A、2 | B、3 | C、5 | D、8 |
命题“若函数f（x）=ex-mx在[0，+∞）上是减函数，则m＞1”的否命题是（ ）
| A、若函数f（x）=ex-mx在[0，+∞）上不是减函数，则m≤1 |
| B、若函数f（x）=ex-mx在[0，+∞）上是减函数，则m≤1 |
| C、若m＞1，则函数f（x）=ex-mx在[0，+∞）上是减函数 |
| D、若m≤1，则函数f（x）=ex-mx在[0，+∞）上不是减函数 |
如果执行如图所示的程序框图，则输出的结果S为（ ）
A、-
| ||
| B、-1 | ||
C、
| ||
| D、0 |
设Sn是等差数列{an}的前n项和，若
=1，则
=（ ）
| S11 |
| S9 |
| a6 |
| a5 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
已知α终边上在直线y=2x上，则1+sinαcosα等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
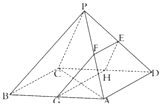如图，四棱锥P-ABCD中，底面ABCD是边长为2