题目内容
已知log2x+log2y=1,则x+y的最小值为 .
考点:基本不等式,对数的运算性质
专题:函数的性质及应用
分析:由log2x+log2y=1,得出xy=2,且x>0,y>0;由基本不等式求出x+y的最小值.
解答:
解:∵log2x+log2y=1,
∴log2(xy)=1,
∴xy=2,其中x>0,y>0;
∴x+y≥2
=2
,当且仅当x=y=
时,“=”成立;
∴x+y的最小值为2
.
故答案为:2
.
∴log2(xy)=1,
∴xy=2,其中x>0,y>0;
∴x+y≥2
| xy |
| 2 |
| 2 |
∴x+y的最小值为2
| 2 |
故答案为:2
| 2 |
点评:本题考查了对数的运算性质以及基本不等式的应用问题,解题时应注意基本不等式的应用条件是什么,是基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
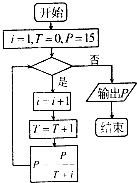 一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )| A、T≤3 | B、T≤4 |
| C、T≤5 | D、T≤6 |