题目内容
已知二次函数f(x)=ax2-x+c同时满足下列二个条件:①f(0)=1,②方程f(x)=x有两个相等的实数根.
(1)求f(x)的解析式;
(2)设h(x)=x2-mx+2,若在区间[1,3]上,f(x)>h(x)恒成立,试确定实数m的取值范围.
(1)求f(x)的解析式;
(2)设h(x)=x2-mx+2,若在区间[1,3]上,f(x)>h(x)恒成立,试确定实数m的取值范围.
考点:二次函数的性质,函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)先求出c,再利用判别式,建立方程,求出a,即可求f(x)的解析式;
(2)利用分离参数法,再求出对应函数在x∈[1,3]上的最大值,即可求m的取值范围.
(2)利用分离参数法,再求出对应函数在x∈[1,3]上的最大值,即可求m的取值范围.
解答:
解:(1)∵f(0)=1,∴c=1;
∵方程f(x)=x有两个相等的实数根,
∴方程ax2-2x+1=0有两个相等的实数根,
∴△=4-4a=0,
∴a=1,
∴f(x)=x2-x+1;
(2)f(x)>h(x),即m>1+
,
∵x∈[1,3],∴1+
∈[
,2],
∵在区间[1,3]上,f(x)>h(x)恒成立,
∴m>2.
∵方程f(x)=x有两个相等的实数根,
∴方程ax2-2x+1=0有两个相等的实数根,
∴△=4-4a=0,
∴a=1,
∴f(x)=x2-x+1;
(2)f(x)>h(x),即m>1+
| 1 |
| x |
∵x∈[1,3],∴1+
| 1 |
| x |
| 4 |
| 3 |
∵在区间[1,3]上,f(x)>h(x)恒成立,
∴m>2.
点评:本题考查恒成立问题,考查分离参数法的运用,解题的关键是分离参数,正确求最值,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的表面积为( )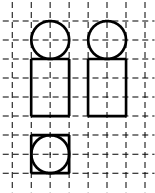

| A、32+4π | ||
| B、24+4π | ||
C、12+
| ||
D、24+
|
函数f(x)=log2(x+1)-
的零点的个数是( )
| 2 |
| x |
| A、0 | B、1 | C、2 | D、3 |