题目内容
在数列{an}中,a1=1,a2=2,an=(-1)n×2an-2(n≥3,n∈N*),其前n项和为Sn.
(1)求a2n+1关于n的表达式;
(2)观察S1,S2,S3,S4,…,Sn,数列{Sn}的前100项中相等的项有几对?
(1)求a2n+1关于n的表达式;
(2)观察S1,S2,S3,S4,…,Sn,数列{Sn}的前100项中相等的项有几对?
考点:数列的求和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)把已知的数列递推式变形,得到数列{an}的所有奇数项构成以1为首项,以-2为公比的等比数列,
所有偶数项构成以2为首项,以2为公比的等比数列.由此可得a2n+1关于n的表达式;
(2)由(1)写出数列{an}的前几项,通过观察可知,S1,S2,S3中有一对相等的,以后每四项有一对,则答案可求.
所有偶数项构成以2为首项,以2为公比的等比数列.由此可得a2n+1关于n的表达式;
(2)由(1)写出数列{an}的前几项,通过观察可知,S1,S2,S3中有一对相等的,以后每四项有一对,则答案可求.
解答:
解:(1)由an=(-1)n×2an-2(n≥3,n∈N*),得
=(-1)n•2,
∴数列{an}的所有奇数项构成以1为首项,以-2为公比的等比数列,
所有偶数项构成以2为首项,以2为公比的等比数列.
∴a2n+1=(-2)n;
(2)由(1)可知,数列{an}的项为:
1,2,-2,4,4,8,-8,16,16,32,-32,…
由上可知,S1,S2,S3中有一对相等的,
以后每四项有一对,共25对.
| an |
| an-2 |
∴数列{an}的所有奇数项构成以1为首项,以-2为公比的等比数列,
所有偶数项构成以2为首项,以2为公比的等比数列.
∴a2n+1=(-2)n;
(2)由(1)可知,数列{an}的项为:
1,2,-2,4,4,8,-8,16,16,32,-32,…
由上可知,S1,S2,S3中有一对相等的,
以后每四项有一对,共25对.
点评:本题考查了等差数列和等比数列的通项公式,考查了学生的归纳推理能力,是中档题.

练习册系列答案
相关题目
已知f(x)是定义在(-∞,+∞)上的增函数,若a∈R,则( )
| A、f(a)>f(2a) |
| B、f(a2)<f(a) |
| C、f(a+3)>f(a-2) |
| D、f(6)>f(a) |
下列各组函数f(x)与g(x)的图象相同的是( )
A、f(x)=x,g(x)=(
| ||||||||||
| B、f(x)=x2,g(x)=(x+1)2 | ||||||||||
C、f(x)=1,g(x)=
| ||||||||||
D、f(x)=|x|,g(x)=
|

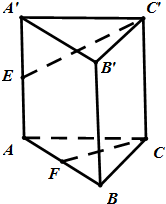 已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.
已知三棱柱ABC-A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点.