题目内容
对于各项均为整数的数列{an},如果ai+i(i=1,2,3,…)为完全平方数,则称数列{an}具有“P性质”,如果数列{an}不具有“P性质”,只要存在与{an}不是同一数列的{bn},且{bn}同时满足下面两个条件:①b1,b2,b3,…bn是a1,a2,a3,…,an的一个排列;②数列{bn}具有“P性质”,则称数列{an}具有“变换P性质”,下面三个数列:①数列1,2,3,4,5;②数列1,2,3,…,11,12;③数列{an}的前n项和为Sn=
(n2-1).其中具有“P性质”或“变换P性质”的有( )
| n |
| 3 |
| A、③ | B、①③ | C、①② | D、①②③ |
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:对于①,数列1,2,3,4,5,具有“变换P性质”,数列{bn}为3,2,1,5,4,具有“P性质”;
对于②,因为11,4都只有与5的和才能构成完全平方数,所以1,2,3,…,11,不具有“变换P性质”;
对于③,求出数列{an}的通项,验证ai+i=i2(i=1,2,3,…)为完全平方数,可得结论
对于②,因为11,4都只有与5的和才能构成完全平方数,所以1,2,3,…,11,不具有“变换P性质”;
对于③,求出数列{an}的通项,验证ai+i=i2(i=1,2,3,…)为完全平方数,可得结论
解答:
解:对于①,数列1,2,3,4,5,具有“变换P性质”,数列{bn}为3,2,1,5,4,具有“P性质”,
∴数列{an}具有“变换P性质”;
对于②,∵11,4都只有与5的和才能构成完全平方数,
∴1,2,3,…,11,不具有“变换P性质”.
对于③,当n≥2时,an=Sn-Sn-1=n2-n
∵a1=0,∴an=n2-n.
∴ai+i=i2(i=1,2,3,…)为完全平方数
∴数列{an}具有“P性质”;
故选:D.
∴数列{an}具有“变换P性质”;
对于②,∵11,4都只有与5的和才能构成完全平方数,
∴1,2,3,…,11,不具有“变换P性质”.
对于③,当n≥2时,an=Sn-Sn-1=n2-n
∵a1=0,∴an=n2-n.
∴ai+i=i2(i=1,2,3,…)为完全平方数
∴数列{an}具有“P性质”;
故选:D.
点评:本题考查新定义,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
相关题目
已知直线l1:x+ky-2k=0与l2:kx-(k-2)y+1=0垂直,则k的值是( )
| A、1 | B、3 | C、1或-2 | D、0或3 |
已知i为虚数单位,若1-bi=
,则a+bi的模等于( )
| 2i |
| a+i |
A、
| ||
| B、2 | ||
| C、4 | ||
| D、1 |
已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X<2)=( )
| A、0.1588 |
| B、0.1587 |
| C、0.1586 |
| D、0.1585 |
“a=-1”是“直线ax+2y+1=0与直线x+(a-1)y-2=0平行”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
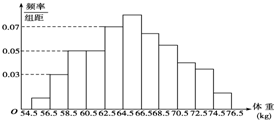 为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是
为了解某地区高三学生的身体发育情况,抽查了该地区100名高三男生的体重.根据抽样测量后的男生体重(单位:kg)数据绘制的频率分布直方图如图所示,则这100名学生中体重值在区间[56.5,64.5)的人数是