题目内容

已知f1（x）=xex，且fn（x）=f′n-1（x）（n∈N，n≥2），则f2014（1）=
 
．
考点：导数的运算
专题：导数的概念及应用
分析：求出函数的导数，计算导数的规律性，即可得到结论．
解答： 解：∵f0（x）=xex，
∴f1（x）=f0′（x）=xex+ex，
f2（x）=f1′（x）=xex+2ex，
f3（x）=f2′（x）=xex+3ex，
…
当n=2014时，f2014（x）=f2013′（x）=xex+2014ex，
此时f2014（1）=2014e1=2014e，
故答案为：2014e
点评：本题主要考查导数的计算，根据导数的公式，得到导数的规律是解决本题的关键．
练习册系列答案
相关题目
国内投寄信函（外埠），邮资按下列规则计算：
（1）信函质量不超过100g时，每20g付邮资80分，即信函质量不超过20g付邮资80分，信函质量超过20g时，但不超过40g付邮资160分，依此类推；
（2）信函质量大于100g且不超过200g时，每100g付邮资200分，即信函质量超过100g，但不超过200g付邮资（A+200）分（A为质量等于100g的信函的邮资），信函质量超过200g，但不超过300g付邮资（A+400）分，依此类推．
设一封xg（0＜x≤200）的信函应付的邮资为y（单位：分），试写出以x为自变量的函数y的解析式，并画出这个函数的图象．
动点P到两点（
3
，0），（-
3
，0）的距离和为4；动点Q在动圆C1：x2+y2=r2（1＜r＜4）上．
（1）求动点P的轨迹C2的方程；
（2）若直线PQ与C1和C2均只有一个交点，求线段PQ长度的最大值．
某几何体的三视图如图所示，说明该简单组合体的结构，并求该几何体的体积．
已知
OA
=（3，1），
OB
=（0，4），
OC
=（x，4），且
AC
⊥
AB
，则x=
 
．
设x，y满足约束条件 
2x-y+2≥0
8x-y-4≤0
x≥0，y≥0
，若目标函数z=abx+y，（a＞0，b＞0）的最大值为10，则a+b的最小值为
 
．
函数f（x）=
x
x+2
在区间[2，4]上的最小值为
 
．
若不等式f（x）≥0的解集为[2，4]，不等式g（x）≥0的解集为∅，则
f(x)
g(x)
＞0的解集为
 
．
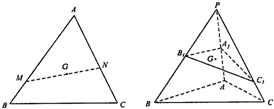如图，已知点G是△ABC的重心（即三角形各边中线的交点），过点G作直线与AB、AC两边分别交于M、N两点，若
AM
=x
AB
，
AN
=y
AC
，则
1
x
+
1
y
=3，由平面图形类比到空间图形，设任一经过三棱锥P-ABC的重心G（即各个面的重心与该面所对顶点连线的交点）的平面分别与三条侧棱交于A1、B1、C1，且
PA1
=x
PA
，
PB1
=y
PB
，
PC1
=z
PC
，则有
1
x
+
1
y
+
1
z
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网