题目内容
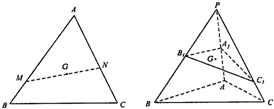如图，已知点G是△ABC的重心（即三角形各边中线的交点），过点G作直线与AB、AC两边分别交于M、N两点，若| AM |
| AB |
| AN |
| AC |
| 1 |
| x |
| 1 |
| y |
| PA1 |
| PA |
| PB1 |
| PB |
| PC1 |
| PC |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
考点：平面向量的基本定理及其意义
专题：计算题,探究型
分析：利用平面的向量表示式，可知存在实数λ，μ，γ，且λ+μ+γ=1，使得
=λ
+μ
+γ
．而
=
(
+
+
)，建立λ，μ，γ与x，y，z的联系，整体构造出
+
+
求解．
| PG |
| PA1 |
| PB1 |
| PC1 |
| PG |
| 3 |
| 4 |
| 1 |
| 3 |
| PA |
| 1 |
| 3 |
| PB |
| 1 |
| 3 |
| PC |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
解答：
解：由于G，A1、B1、C1，四点共面，所以存在实数λ，μ，γ，且λ+μ+γ=1，
使得
=λ
+μ
+γ
=λx
+μy
+γz
而
=
(
+
+
)，所以
，
从而λ+μ+γ=4（
+
+
）=1，所以
+
+
=4
故答案为：4．
使得
| PG |
| PA1 |
| PB1 |
| PC1 |
| PA |
| PB |
| PC |
而
| PG |
| 3 |
| 4 |
| 1 |
| 3 |
| PA |
| 1 |
| 3 |
| PB |
| 1 |
| 3 |
| PC |
|
从而λ+μ+γ=4（
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
故答案为：4．
点评：本题考查空间向量的表示，向量共面的性质．思维难度较大．
练习册系列答案
相关题目