题目内容
已知函数f(x)=ex-ax-1(a>0,e为自然对数的底数).
(1)若f(x)≥0对任意的x∈R恒成立,求实数a的值;
(2)在(1)的条件下,证明:(
)n+(
)n+…+(
)n+(
)n<
(n∈N*)
(1)若f(x)≥0对任意的x∈R恒成立,求实数a的值;
(2)在(1)的条件下,证明:(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| e |
| e-1 |
考点:导数在最大值、最小值问题中的应用
专题:计算题,证明题,导数的综合应用
分析:(1)f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)min≥0.构造函数g(a)=a-alna-1,所以g(a)≥0,确定函数的单调性,即可求得实数a的值;
(2)由(1)知,当x>0时,ex>x+1,即ex>x,则1>ln2,
>ln(1+
),
>ln(1+
),…,
>ln(1+
),累加再由对数的运算法则,即可得证.
(2)由(1)知,当x>0时,ex>x+1,即ex>x,则1>ln2,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n |
解答:
(1)解:f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)min≥0.
由题意a>0,f′(x)=ex-a,
由f′(x)=ex-a=0,得x=lna.
当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.
则f(x)在(-∞,lna)单调递减,在(lna,+∞)单调递增.
设g(a)=a-alna-1,所以g(a)≥0.
由g′(a)=1-lna-1=-lna=0得a=1.
则g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴g(a)在a=1处取得最大值,而g(1)=0.
因此g(a)≥0的解为a=1,故a=1;
(2)证明:由(1)可知:当x>0时,ex>x+1,即ex>x,
即有enx>xn.
则(
)n<e,(
)n<e2,(
)n<e3,…,(
)n<en,
则(
)n+(
)n+…+(
)n+(
)n<e+e2+e3+…+en=
<
故(
)n+(
)n+…+(
)n+(
)n<
成立.
由题意a>0,f′(x)=ex-a,
由f′(x)=ex-a=0,得x=lna.
当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.
则f(x)在(-∞,lna)单调递减,在(lna,+∞)单调递增.
设g(a)=a-alna-1,所以g(a)≥0.
由g′(a)=1-lna-1=-lna=0得a=1.
则g(a)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
∴g(a)在a=1处取得最大值,而g(1)=0.
因此g(a)≥0的解为a=1,故a=1;
(2)证明:由(1)可知:当x>0时,ex>x+1,即ex>x,
即有enx>xn.
则(
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n |
| n |
则(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| e(1-en) |
| 1-e |
| e |
| e-1 |
故(
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
| e |
| e-1 |
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,同时考查不等式的证明,解题的关键是正确求导数,确定函数的单调性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
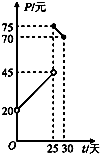 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表: