题目内容
7.已知a∈R,则“a<0”是“|x|+|x+1|>a恒成立”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 |x|+|x+1|≥|x-(x+1)|=1,|x|+|x+1|>a恒成立,可得a<1.即可得出.
解答 解:∵|x|+|x+1|≥|x-(x+1)|=1,|x|+|x+1|>a恒成立,
∴a<1.
∴“a<0”是“|x|+|x+1|>a恒成立”的充分不必要条件.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
2.已知点P在抛物线y2=x上,点Q在圆(x+$\frac{1}{2}$)2+(y-4)2=1上,则|PQ|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}-1$ | B. | $\frac{{3\sqrt{3}}}{2}-1$ | C. | $2\sqrt{3}-1$ | D. | $\sqrt{10}-1$ |
17.若实数a,b均不为零,且x2a=$\frac{1}{x^b}$(x>0),则(xa-2xb)9展开式中的常数项等于( )
| A. | 672 | B. | -672 | C. | -762 | D. | 762 |
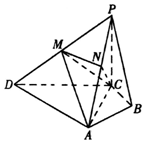 在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC.
在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC. 如图,已知函数y=2kx(k>0)与函数y=x2的图象所围成的阴影部分的面积为$\frac{32}{3}$,则实数k的值为2.
如图,已知函数y=2kx(k>0)与函数y=x2的图象所围成的阴影部分的面积为$\frac{32}{3}$,则实数k的值为2.