题目内容
设函数f(x)=
(x>0),且f1(x)=f(x)=
,当n∈N*且n≥2时,fn(x)=f[fn-1(x)],则f3(x)= ,猜想fn(x)(n∈N*)的表达式为 .
| x |
| x+2 |
| x |
| x+2 |
考点:归纳推理,函数解析式的求解及常用方法
专题:函数的性质及应用,推理和证明
分析:由题意依次求出f2(x)、f3(x)、f4(x)的表达式,利用规律性猜想出fn(x)(n∈N*)的表达式.
解答:
解:因为f1(x)=f(x)=
,当n≥2时,fn(x)=f[fn-1(x)],
所以f2(x)=f[f1(x)]=
=
,
f3(x)=f[f2(x)]=
=
,
f4(x)=f[f3(x)]=
=
,
由以上的式子猜想fn(x)=
,
故答案为:
;fn(x)=
(n∈N*).
| x |
| x+2 |
所以f2(x)=f[f1(x)]=
| ||
|
| x |
| 3x+4 |
f3(x)=f[f2(x)]=
| ||
|
| x |
| 7x+8 |
f4(x)=f[f3(x)]=
| ||
|
| x |
| 15x+16 |
由以上的式子猜想fn(x)=
| x |
| (2n-1)x+2n |
故答案为:
| x |
| 7x+8 |
| x |
| (2n-1)x+2n |
点评:本题考查归纳推理,函数解析式的求解,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )| A、π | B、2π | C、3π | D、4π |
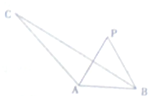 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.