题目内容
已知函数f(x)=2x2-3x+1.
(1)当0≤x≤
时,求y=f(sinx)的最大值;
(2)问a取何值时,方程f(sinx)=a-sinx在[0,2π)上有两解?
(1)当0≤x≤
| π |
| 2 |
(2)问a取何值时,方程f(sinx)=a-sinx在[0,2π)上有两解?
考点:二次函数的性质,函数零点的判定定理
专题:分类讨论,函数思想,方程思想,换元法,函数的性质及应用,三角函数的图像与性质
分析:(1)根据函数f(x)得出y=f(sinx)的解析式,用换元法,设t=sinx,x∈[0,
],求出f(t)在区间[0,1]上的最值即可;
(2)把方程f(sinx)=a-sinx转化为2sin2x-2sinx+1=a在[0,2π]上有两解的问题,用换元法,求方程2t2-2t+1=a在[-1,1]上解的情况即可.
| π |
| 2 |
(2)把方程f(sinx)=a-sinx转化为2sin2x-2sinx+1=a在[0,2π]上有两解的问题,用换元法,求方程2t2-2t+1=a在[-1,1]上解的情况即可.
解答:
解:(1)∵函数f(x)=2x2-3x+1,
∴y=f(sinx)=2sin2x-3sinx+1,
设t=sinx,x∈[0,
],则0≤t≤1,
∴y=2(t2-
t)+1=2(t-
)2-
,
∴当t=0时,函数y取得最大值ymax=1;
(2)∵方程f(sinx)=a-sinx,
∴2sin2x-3sinx+1=a-sinx,
即2sin2x-2sinx+1=a在[0,2π]上有两解,
设t=sinx,则
2t2-2t+1=a在[-1,1]上解的情况如下;
①当方程在(-1,1)上只有一个解或相等解时,
x有两解(5-a)(1-a)<0或△=0;
∴a∈(1,5)或a=
;
②当t=-1时,x有唯一解x=
π,
③当t=1时,x有唯一解x=
;
综上,当a∈(1,5)或a=
时,方程f(sinx)=a-sinx在[0,2π)上有两解.
∴y=f(sinx)=2sin2x-3sinx+1,
设t=sinx,x∈[0,
| π |
| 2 |
∴y=2(t2-
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 8 |
∴当t=0时,函数y取得最大值ymax=1;
(2)∵方程f(sinx)=a-sinx,
∴2sin2x-3sinx+1=a-sinx,
即2sin2x-2sinx+1=a在[0,2π]上有两解,
设t=sinx,则
2t2-2t+1=a在[-1,1]上解的情况如下;
①当方程在(-1,1)上只有一个解或相等解时,
x有两解(5-a)(1-a)<0或△=0;
∴a∈(1,5)或a=
| 1 |
| 2 |
②当t=-1时,x有唯一解x=
| 3 |
| 2 |
③当t=1时,x有唯一解x=
| π |
| 2 |
综上,当a∈(1,5)或a=
| 1 |
| 2 |
点评:本题考查了函数的图象与性质的应用问题,也考查了三角函数的图象与性质,考查了函数与方程的应用问题,考查了换元法的应用问题,是综合性题目.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知α,β均为锐角,sinα=
,cosβ=
,求α-β为( )
| ||
| 5 |
| ||
| 10 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
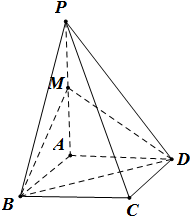 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=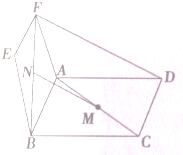 如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.
如图,已知?ABCD与?ABEF共边于AB,M,N分别在对角线AC,BF上,且AM:AC=FN:FB.求证:MN∥平面ADF.