题目内容
已知f(x)=(ax2+(a-1)2x-a2+3a-12)ex,a≥0,g(x)=lnx-x-3.
(1)求g(x)的最大值;
(2)若函数f(x)在区间(2,3)上单调,求a的取值范围;
(3)当a=0时,设h(x)=
+g(x),若直线y=kx+b与曲线y=h(x)的交点为A(x1,y1),B(x2,y2),其中0<x1<x2,证明:k(x1+x2)>2成立.
(1)求g(x)的最大值;
(2)若函数f(x)在区间(2,3)上单调,求a的取值范围;
(3)当a=0时,设h(x)=
| f(x) |
| ex |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)g′(x)=
-1=
,分别解出g′(x)>0,g′(x)<0,即可得出g(x)单调性与极值.
(2)f′(x)=[ax2+(a2+1)x+a-11]ex,对a分类讨论:当a=0时,当a>0时,记u(x)=ax2+(a2+1)x+a-11,利用二次函数的单调性及其导数与函数的单调性即可得出.
(3)当a=0时,设h(x)=
+g(x)=lnx-15,k=
=
,要证明k(x1+x2)>2成立.即证明
(x2+x1)>2成立,即证明
ln
>2成立,令t=
>1,上式即证明
lnt>2成立,记v(t)=(t+1)lnt-2(t-1),利用导数研究其单调性极值即可得出.
| 1 |
| x |
| 1-x |
| x |
(2)f′(x)=[ax2+(a2+1)x+a-11]ex,对a分类讨论:当a=0时,当a>0时,记u(x)=ax2+(a2+1)x+a-11,利用二次函数的单调性及其导数与函数的单调性即可得出.
(3)当a=0时,设h(x)=
| f(x) |
| ex |
| h(x2)-h(x1) |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
| ||
|
| x2 |
| x1 |
| x2 |
| x1 |
| t+1 |
| t-1 |
解答:
解:(1)g′(x)=
-1=
,
当0<x<1时,g′(x)>0,g(x)单调递增;
当1<x时,g′(x)<0,g(x)单调递减.
∴g(x)max=g(1)=-4.
(2)f′(x)=[ax2+(a2+1)x+a-11]ex,
当a=0时,f′(x)=(x-11)ex在区间(2,3)上单调递减,符合题意;
当a>0时,记u(x)=ax2+(a2+1)x+a-11,对称轴为x=-
<0,
要使f(x)在区间(2,3)上单调,只需要u(2)≥0或u(3)≤0,即
或
,解得a≥
或0<a≤
.
综上可得:a的取值范围是(0,
]∪[
,+∞).
(3)当a=0时,设h(x)=
+g(x)=lnx-15,k=
=
,
要证明k(x1+x2)>2成立.即证明
(x2+x1)>2成立,即证明
ln
>2成立,
令t=
>1,上式即证明
lnt>2成立,记v(t)=(t+1)lnt-2(t-1),
v′(t)=lnt+
-1,v′(1)=0,
v″(t)=
-
=
>0在t>1时恒成立.
∴v′(t)在t>1时单调递增,v′(t)>v′(1)=0.
∴v(t)在(1,+∞)上单调递增,
∴v(t)>v(1)=0.即当t>1时,v(t)>0恒成立.
因此k(x1+x2)>2成立.
| 1 |
| x |
| 1-x |
| x |
当0<x<1时,g′(x)>0,g(x)单调递增;
当1<x时,g′(x)<0,g(x)单调递减.
∴g(x)max=g(1)=-4.
(2)f′(x)=[ax2+(a2+1)x+a-11]ex,
当a=0时,f′(x)=(x-11)ex在区间(2,3)上单调递减,符合题意;
当a>0时,记u(x)=ax2+(a2+1)x+a-11,对称轴为x=-
| a2+1 |
| 2a |
要使f(x)在区间(2,3)上单调,只需要u(2)≥0或u(3)≤0,即
|
|
| ||
| 4 |
| 2 |
| 3 |
综上可得:a的取值范围是(0,
| 2 |
| 3 |
| ||
| 4 |
(3)当a=0时,设h(x)=
| f(x) |
| ex |
| h(x2)-h(x1) |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
要证明k(x1+x2)>2成立.即证明
| lnx2-lnx1 |
| x2-x1 |
| ||
|
| x2 |
| x1 |
令t=
| x2 |
| x1 |
| t+1 |
| t-1 |
v′(t)=lnt+
| 1 |
| t |
v″(t)=
| 1 |
| t |
| 1 |
| t2 |
| t-1 |
| t2 |
∴v′(t)在t>1时单调递增,v′(t)>v′(1)=0.
∴v(t)在(1,+∞)上单调递增,
∴v(t)>v(1)=0.即当t>1时,v(t)>0恒成立.
因此k(x1+x2)>2成立.
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
组合式
-2
+4
-8
+…+(-2)n
的值等于( )
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| A、(-1)n |
| B、1 |
| C、3n |
| D、3n-1 |
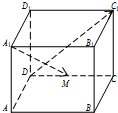 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则| A1M |
| DC1 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
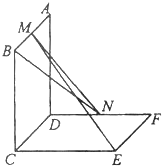 如图,已知两个正方形ABCD 和DCEF不在同一平面内,且平面ABCD⊥平面DCEF,M,N分别为AB,DF的中点.
如图,已知两个正方形ABCD 和DCEF不在同一平面内,且平面ABCD⊥平面DCEF,M,N分别为AB,DF的中点.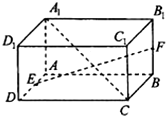 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.