题目内容
已知a,b,c为△ABC的内角A,B,C的对边,且b<a<c,满足
=
,函数f(x)=sinωx(ω>0)在区间[0,
]上单调递增,在区间[
,
]上单调递减.
(1)证明:b,a,c成等差数列;
(2)若f(
)=cosA,且a=2,求△ABC的面积.
| sinB+sinC |
| sinA |
| 2-cosB-cosC |
| cosA |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
(1)证明:b,a,c成等差数列;
(2)若f(
| π |
| 9 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)通过已知表达式,去分母化简,利用两角和与差的三角函数,化简表达式通过正弦定理直接推出b+c=2a;
(2)利用函数的周期求出ω,通过f(
)=cosA,求出A,由余弦定理可解得b,c的值,从而由三角形面积公式即可得解.
(2)利用函数的周期求出ω,通过f(
| π |
| 9 |
解答:
(本小题满分12分)
解:(1)∵
=
,
∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA
=sin(A+B)+sin(A+C)
=2sinA…(3分)
所以sinC+sinB=2sinA…(5分)
所以b+c=2a,即有b,a,c成等差数列.…(6分)
(2)由题意知:由题意知:
=
,解得:ω=
,…(8分)
因为f(
)=sin
=
=cosA,A∈(0,π),所以A=
…(9分)
由余弦定理知:cosA=
=
…(10分)
所以b2+c2-a2=bc因为b+c=2a,所以b2+c2-(
)2=bc,
即:b2+c2-2bc=0所以b=c…(11分)
所以可解得:b=c=2,从而有:S△ABC=
bcsinA=
×2×2×
=
.…(12分)
解:(1)∵
| sinB+sinC |
| sinA |
| 2-cosB-cosC |
| cosA |
∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA
=sin(A+B)+sin(A+C)
=2sinA…(3分)
所以sinC+sinB=2sinA…(5分)
所以b+c=2a,即有b,a,c成等差数列.…(6分)
(2)由题意知:由题意知:
| 2π |
| ω |
| 4π |
| 3 |
| 3 |
| 2 |
因为f(
| π |
| 9 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
由余弦定理知:cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
所以b2+c2-a2=bc因为b+c=2a,所以b2+c2-(
| b+c |
| 2 |
即:b2+c2-2bc=0所以b=c…(11分)
所以可解得:b=c=2,从而有:S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题主要考查三角函数的化简求值,两角和与差的三角函数,正弦定理与余弦定理及三角形面积公式的应用,属于基本知识的考查.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
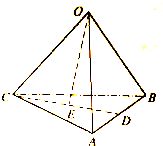 如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设
如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
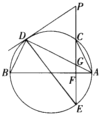 如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.
如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.