题目内容
已知无穷整数数集A={a1,a2,a3,…,an,…}(a1<a2<a3<…<an<…)具有性质P:对任意互不相等的正整数i,j,k,总有ai+|ak-aj|∈A.
(Ⅰ)若{1,21}⊆A且5∉A,判断13是否属于A,并说明理由;
(Ⅱ)求证:a1,a2,a3,…,an,…是等差数列;
(Ⅲ)已知x,y∈N且y>x>0,记 M是满足{0,x,y}⊆A的数集A中的一个,且是满足{0,x,y}⊆A的所有数集A的子集,求证:x,y互质是M=N的充要条件.
(Ⅰ)若{1,21}⊆A且5∉A,判断13是否属于A,并说明理由;
(Ⅱ)求证:a1,a2,a3,…,an,…是等差数列;
(Ⅲ)已知x,y∈N且y>x>0,记 M是满足{0,x,y}⊆A的数集A中的一个,且是满足{0,x,y}⊆A的所有数集A的子集,求证:x,y互质是M=N的充要条件.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(Ⅰ)13∉A,利用反证法即可判断;
(Ⅱ)ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,可得ak+1=ak+ak+2-ak+1,即可证明结论;
(Ⅲ)设ai=0,aj=x,ak=y,i<j<k,则y=(k-i)d,x=(j-i)d,分充分性、必要性证明即可.
(Ⅱ)ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,可得ak+1=ak+ak+2-ak+1,即可证明结论;
(Ⅲ)设ai=0,aj=x,ak=y,i<j<k,则y=(k-i)d,x=(j-i)d,分充分性、必要性证明即可.
解答:
(Ⅰ)解:13∉A.
设13∈A,则由{1,21}⊆A,性质P可得1+|13-9|=5∈A,与5∉A矛盾,∴13∉A;
(Ⅱ)证明:对任意k+2≤n,由性质P可得ak+ak+2-ak+1∈A,
∵ak<ak+1<ak+2,
∴ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,
∴ak+1=ak+ak+2-ak+1,
∴2ak+1=ak+ak+2,
∴a1,a2,a3,…,an是等差数列;
(Ⅲ)解:由(Ⅱ)可知,a1,a2,a3,…,an公差为d,且d∈Z
设ai=0,aj=x,ak=y,i<j<k,则y=(k-i)d,x=(j-i)d,
首先证明:x,y互质是M=N的充分条件.
∵x,y互质,∴d=1,
∵M是满足{0,x,y}⊆A的所有数集A的子集,
∴M=N;
其次证明x,y互质是M=N的必要条件.
假设x,y不互质,则x,y有大于1的因数p,
∴满足条件A={a1,a2,a3,…,an,…}中的元素所构成的数列a1,a2,a3,…,an,…的公差d可以取1,也可以取p,
此时A={0,p,2p,…,(n-1)p,…}满足条件,且={0,p,2p,…,(n-1)p,…}?N,
与M=N矛盾,
∴x,y互质,
∴x,y互质是M=N的充要条件.
设13∈A,则由{1,21}⊆A,性质P可得1+|13-9|=5∈A,与5∉A矛盾,∴13∉A;
(Ⅱ)证明:对任意k+2≤n,由性质P可得ak+ak+2-ak+1∈A,
∵ak<ak+1<ak+2,
∴ak+ak+2-ak+1∈A且ak<ak+ak+2-ak+1<ak+2,
∴ak+1=ak+ak+2-ak+1,
∴2ak+1=ak+ak+2,
∴a1,a2,a3,…,an是等差数列;
(Ⅲ)解:由(Ⅱ)可知,a1,a2,a3,…,an公差为d,且d∈Z
设ai=0,aj=x,ak=y,i<j<k,则y=(k-i)d,x=(j-i)d,
首先证明:x,y互质是M=N的充分条件.
∵x,y互质,∴d=1,
∵M是满足{0,x,y}⊆A的所有数集A的子集,
∴M=N;
其次证明x,y互质是M=N的必要条件.
假设x,y不互质,则x,y有大于1的因数p,
∴满足条件A={a1,a2,a3,…,an,…}中的元素所构成的数列a1,a2,a3,…,an,…的公差d可以取1,也可以取p,
此时A={0,p,2p,…,(n-1)p,…}满足条件,且={0,p,2p,…,(n-1)p,…}?N,
与M=N矛盾,
∴x,y互质,
∴x,y互质是M=N的充要条件.
点评:本题考查数列的应用,考查学生对新定义的理解,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
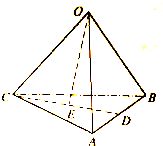 如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设
如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
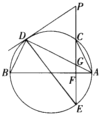 如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.
如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.