题目内容
等差数列{an}中,前n项和用Sn表示,已知S5=35,S10=120.求:
(1)Sn;
(2)an.
(1)Sn;
(2)an.
考点:等差数列的性质
专题:等差数列与等比数列
分析:(1)利用等差数列的求和公式和已知条件列方程求得a1和d,利用等差数列的求和公式求得答案.
(2)根据等差数列的求和公式求得数列的通项公式.
(2)根据等差数列的求和公式求得数列的通项公式.
解答:
解:依题意
求得a1=3,d=2,
(1)Sn=3n+
×2=n2+2n,.
(2)an=3+(n-1)×2=2n+1.
|
(1)Sn=3n+
| n(n-1) |
| 2 |
(2)an=3+(n-1)×2=2n+1.
点评:本题主要考查了等差数列的性质.特别是对等差数列求和公式和通项公式的运用.

练习册系列答案
相关题目
已知2m+n=1,其中m,n均为正数,则
+
的最小值为( )
| 1 |
| m |
| 2 |
| n |
| A、2 | B、4 | C、8 | D、16 |
如图程序运行后的输出结果为( )


| A、17 | B、21 | C、23 | D、25 |
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m⊥β,m∥α,则α⊥β |
| B、若m?β,α⊥β,则m⊥α |
| C、若m∥α,n∥β,α∥β,则m∥n |
| D、若m?α,n?β,m∥n,则α∥β |
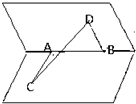 二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的量两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2
二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的量两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2