题目内容
f(x)是定义在R上的奇函数,x>0时,f(x)=x2+(2-a)x,a≥0,若对任意x∈R,都有f(x-
a)≤f(x),则a的范围是 .
| 2 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用,导数的综合应用
分析:x>0时,f′(x)=2x+2-a,所以0≤a≤2时,对于x>0时的函数f(x)是增函数,根据奇函数图象在对称区间上的单调性及经过原点的情况即可判断出f(x)在R上单调递增,所以便能得到f(x-
a)≤f(x);a>2时,画出f(x)及f(x-
a)的图象,通过图象即可看出a满足的范围,所以对以上两种情况的a的范围求并集即可.
| 2 |
| 2 |
解答:
解:f′(x)=2x+2-a;
∴①0≤a≤2,且x>0时,f′(x)>0;
∴f(x)在(0,+∞)上单调递增;
∵f(x)在R上是奇函数,f(0)=0,且(0,0)满足x>0时的解析式f(x);
∴函数f(x)在R上是增函数;
又a≥0,x-
a≤x;
∴对任意x∈R,f(x-
a)≤f(x);
②a>2时,f(x)=0有两实根x=0,a-2,根据f(x)是奇函数,及x>0时的解析式及平移的知识画出f(x),f(x-
a)的图象如下:
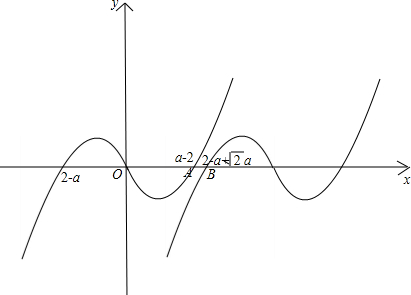
由图象可已看出B点应在A点右边或与A重合;
∴2-a+
a≥a-2;
解得a≤2(2+
);
∴2<a≤2(2+
);
综上得a的取值范围为[0,2(2+
)].
故答案为:[0,2(2+
)].
∴①0≤a≤2,且x>0时,f′(x)>0;
∴f(x)在(0,+∞)上单调递增;
∵f(x)在R上是奇函数,f(0)=0,且(0,0)满足x>0时的解析式f(x);
∴函数f(x)在R上是增函数;
又a≥0,x-
| 2 |
∴对任意x∈R,f(x-
| 2 |
②a>2时,f(x)=0有两实根x=0,a-2,根据f(x)是奇函数,及x>0时的解析式及平移的知识画出f(x),f(x-
| 2 |

由图象可已看出B点应在A点右边或与A重合;
∴2-a+
| 2 |
解得a≤2(2+
| 2 |
∴2<a≤2(2+
| 2 |
综上得a的取值范围为[0,2(2+
| 2 |
故答案为:[0,2(2+
| 2 |
点评:考查奇函数的定义,奇函数在对称区间上的单调性,通过判断导数符号判断函数单调性的方法,根据单调性的定义比较两函数值大小的方法,平移的知识,以及数形结合的解题方法.

练习册系列答案
相关题目
已知α、β是两个不同的平面,a、b、c是三条不同的直线,则下列命题正确的( )
| A、若a?α,b∥a,则b∥α |
| B、若a?α,b?α,c?β,a∥c,b∥c,则α∥β |
| C、若a?α,b?α,c?β,c⊥a,c⊥b,则α⊥β |
| D、若a?α,b?α,a∩b≠ϕ,c⊥a,c⊥b,c∥β,则α⊥β |
 如图四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2
如图四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2 如图,椭圆C:
如图,椭圆C: