题目内容
已知函数f(x)=x-
(k∈R)过点(2,0)
(1)判断函数f(x)在(0,+∞)上的单调性并证明;
(2)讨论关于x的方程|f(x)|=t+
x(t∈R)的正根的个数.
| k |
| x |
(1)判断函数f(x)在(0,+∞)上的单调性并证明;
(2)讨论关于x的方程|f(x)|=t+
| 5 |
| 4 |
考点:根的存在性及根的个数判断,函数单调性的判断与证明,函数与方程的综合运用
专题:计算题,分类讨论,函数的性质及应用
分析:(1)求出k=4,直接利用函数的单调性的定义证明函数f(x)在(0,+∞)上的单调性;
(2)由于函数f(x)=x-
在(0,+∞)上单调递增,f(2)=0,故当0<x<2时,f(x)<0;当x>2时,f(x)>0.画出y=|f(x)|和y=t+
x的图象,讨论两图象交点的个数,即可得到关于x的方程|f(x)|=t+
x(t∈R)的正根的个数.
(2)由于函数f(x)=x-
| 4 |
| x |
| 5 |
| 4 |
| 5 |
| 4 |
解答:
解:(1)函数f(x)=x-
(k∈R)图象过点(2,0),
则0=2-
,解得,k=4.
则当k=4时,函数f(x)=x-
在(0,+∞)单调递增.
证明:?x1,x2∈(0,+∞)且x1<x2,则f(x1)-f(x2)=x1-
-x2+
=(x1-x2)-
=(x1-x2)(1+
),
∵x1,x2∈(0,+∞),∴1+
>0.
∵x1<x2,∴x1-x2<0.∴f(x1)-f(x2)<0,
即f(x1)<f(x2).
则函数f(x)在(0,+∞)单调递增;
(2)函数f(x)=x-
,方程|f(x)|=t+
x,即|x-
|=t+
x,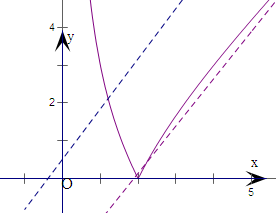
由于函数f(x)=x-
在(0,+∞)上单调递增,
f(2)=0,
故当0<x<2时,f(x)<0;当x>2时,f(x)>0.
当0<x<2时,方程即
-x=t+
x,即 t=
-
x,
显然函数t为减函数,故有t>-
;
当x≥2时,方程即 x-
=t+
x,
即t=-(
+
)≤-2,
故当t<-
或t>-2时,方程有一正根;
当t=-
或t=-2时,方程有二个正根;
当-
<t<-2时,方程有三个正根.
| k |
| x |
则0=2-
| k |
| 2 |
则当k=4时,函数f(x)=x-
| 4 |
| x |
证明:?x1,x2∈(0,+∞)且x1<x2,则f(x1)-f(x2)=x1-
| 4 |
| x1 |
| 4 |
| x2 |
| 4(x2-x1) |
| x1x2 |
| 4 |
| x1x2 |
∵x1,x2∈(0,+∞),∴1+
| 4 |
| x1x2 |
∵x1<x2,∴x1-x2<0.∴f(x1)-f(x2)<0,
即f(x1)<f(x2).
则函数f(x)在(0,+∞)单调递增;
(2)函数f(x)=x-
| 4 |
| x |
| 5 |
| 4 |
| 4 |
| x |
| 5 |
| 4 |

由于函数f(x)=x-
| 4 |
| x |
f(2)=0,
故当0<x<2时,f(x)<0;当x>2时,f(x)>0.
当0<x<2时,方程即
| 4 |
| x |
| 5 |
| 4 |
| 4 |
| x |
| 9 |
| 4 |
显然函数t为减函数,故有t>-
| 5 |
| 2 |
当x≥2时,方程即 x-
| 4 |
| x |
| 5 |
| 4 |
即t=-(
| x |
| 4 |
| 4 |
| x |
故当t<-
| 5 |
| 2 |
当t=-
| 5 |
| 2 |
当-
| 5 |
| 2 |
点评:本题考查函数的单调性及运用,考查绝对值函数的图象和性质,考查分离参数和数形结合的思想方法,属于中档题和易错题.

练习册系列答案
相关题目
直线3x+y-a=0与6x+2y+1=0的位置关系是( )
| A、相交 | B、平行 |
| C、重合 | D、平行或重合 |
设集合A={x|-3<x<3},B={y|y=-x2+t},若A∩B=∅,则实数t的取值范围是( )
| A、t≤-3 | B、t<3 |
| C、t>3 | D、t≥3 |
“a=5”是“直线ax-2y-1=0与直线5x-2y+c=0平行”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
设a=
dx,则
sinxdx=( )
| ∫ | 2 0 |
| 4-x2 |
| ∫ | a 0 |
| A、2π | B、π | C、2 | D、1 |
已知数列{an},定直线l:(m+3)x-(2m+4)y-m-9=0,若(n,an)在直线l上,则数列{an}的前13项和为( )
| A、10 | B、21 | C、39 | D、78 |
光线从点A(-2,
)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2
),则光线BC所在直线的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|