题目内容
经过两点A(4,2y+1),B(2,-3)的直线的斜率为-1,则y等于( )
| A、-1 | B、-3 | C、0 | D、2 |
考点:直线的斜率
专题:直线与圆
分析:利用直线的斜率公式求解.
解答:
解:∵经过两点A(4,2y+1),B(2,-3)的直线的斜率为-1,
∴
=-1,
解得y=-3.
故选:B.
∴
| 2y+1-(-3) |
| 4-2 |
解得y=-3.
故选:B.
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意斜率计算公式的灵活运用.

练习册系列答案
相关题目
观察下列算式:
13=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
…
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n=( )
13=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
…
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n=( )
| A、41 | B、43 | C、45 | D、47 |
直线2x-y+1=0不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图所示,P、Q分别在BC和AC上,BP:CP=2:5,CQ:QA=3:4,则
( )
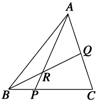
| AR |
| RP |

| A、3:14 | B、14:3 |
| C、17:3 | D、17:14 |
已知函数y=x3+ax在区间(-∞,1)上为减函数,在(1,+∞)上为增函数,则a的值为( )
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|