题目内容
已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率等于
,它的一个顶点B恰好是抛物线x2=4y的焦点.
(1)求椭圆C的方程;
(2)直线l与椭圆C交于M,N两点,那么椭圆C的右焦点F是否可以成为△BMN的垂心?若可以,求出直线l的方程;若不可以,请说明理由.(注:垂心是三角形三条高线的交点)
| ||
| 2 |
(1)求椭圆C的方程;
(2)直线l与椭圆C交于M,N两点,那么椭圆C的右焦点F是否可以成为△BMN的垂心?若可以,求出直线l的方程;若不可以,请说明理由.(注:垂心是三角形三条高线的交点)
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)抛物线x2=4y的焦点为(0,1),可得c=1.再利用
,即可得出.
(2)利用三角形垂心的性质、相互垂直的直线斜率之间的关系可得直线l的斜率为1.设直线的方程为y=x+m,代入椭圆方程并整理,可得3x2+4bx+2(b2-1)=0.设M(x1,y1),N(x2,y2),利用根与系数的关系、向量垂直与数量积的关系即可得出.
|
(2)利用三角形垂心的性质、相互垂直的直线斜率之间的关系可得直线l的斜率为1.设直线的方程为y=x+m,代入椭圆方程并整理,可得3x2+4bx+2(b2-1)=0.设M(x1,y1),N(x2,y2),利用根与系数的关系、向量垂直与数量积的关系即可得出.
解答:
解:(1)设椭圆方程为
+
=1(a>b>0),
抛物线x2=4y的焦点为(0,1),
由
⇒a=
,
∴椭圆方程为
+y2=1.
(2)假设存在直线l,使得点F是△BMN的垂心.
易知直线BF的斜率为-1,从而直线l的斜率为1.
设直线的方程为y=x+m,代入椭圆方程并整理,可得3x2+4mx+2(m2-1)=0.
设M(x1,y1),N(x2,y2),
则x1+x2=-
m,x1x2=
.
于是
•
=(1-x2)x1-y2(y1-1)
=x1+y2-x1x2-y1y2
=x1+x2+m-x1x2-(x1+m)(x2+m)
=-2x1x2+(1-m)(x1+x2)+m-m2
=
+(1-m)(-
)+m-m2=0,
解之得m=1或m=-
.
当m=1时,点B即为直线l与椭圆的交点,不合题意;
当m=-
时,经检验符合题意.
∴当且仅当直线l的方程为y=x-
时,点F是△BMN的垂心.
| x2 |
| a2 |
| y2 |
| b2 |
抛物线x2=4y的焦点为(0,1),
由
|
| 2 |
∴椭圆方程为
| x2 |
| 2 |
(2)假设存在直线l,使得点F是△BMN的垂心.
易知直线BF的斜率为-1,从而直线l的斜率为1.
设直线的方程为y=x+m,代入椭圆方程并整理,可得3x2+4mx+2(m2-1)=0.
设M(x1,y1),N(x2,y2),
则x1+x2=-
| 4 |
| 3 |
| 2m2-2 |
| 3 |
于是
| NF |
| BM |
=x1+y2-x1x2-y1y2
=x1+x2+m-x1x2-(x1+m)(x2+m)
=-2x1x2+(1-m)(x1+x2)+m-m2
=
| -2(2m2-2) |
| 3 |
| 4m |
| 3 |
解之得m=1或m=-
| 4 |
| 3 |
当m=1时,点B即为直线l与椭圆的交点,不合题意;
当m=-
| 4 |
| 3 |
∴当且仅当直线l的方程为y=x-
| 4 |
| 3 |
点评:本题考查了椭圆与抛物线的标准方程及其性质、三角形垂心的性质、相互垂直的直线斜率之间的关系、直线与椭圆相交问题转化为方程联立可得根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;
②若m∥α,n∥α,则m∥n;
③若α∥β,β∥γ,m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β;
其中正确命题的序号是( )
①若m⊥α,n∥α,则m⊥n;
②若m∥α,n∥α,则m∥n;
③若α∥β,β∥γ,m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β;
其中正确命题的序号是( )
| A、①和③ | B、②和③ |
| C、②和④ | D、①和④ |
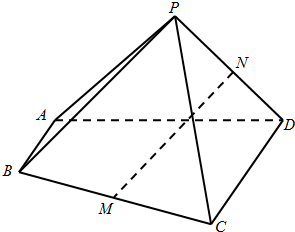 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.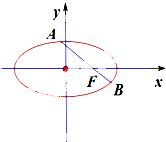 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆