题目内容
已知椭圆
+
=1上一点P与椭圆两个焦点连线互相垂直，求点P的坐标．
| x2 |
| 45 |
| y2 |
| 20 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：以椭圆的中心为圆心，以半焦距为半径的圆，椭圆与圆的交点即为所求．
解答：
解：∵椭圆
+
=1
∴a2=45，b2=20，
c2=a2-b2=25
以O为圆心，半径5的圆方程
x2+y2=25 （1）
+
=1 （2）
由（1）（2）得：
x2=9，y2=9
解得：x1=-3，x2=3，y1=4，y2=-4，
椭圆
+
=1上一点P与椭圆两个焦点连线互相垂直，
即椭圆与圆的交点，
所以交点坐标是（-3，-4），（-3，4），（3，-4），（3，4）．
| x2 |
| 45 |
| y2 |
| 20 |
∴a2=45，b2=20，
c2=a2-b2=25
以O为圆心，半径5的圆方程
x2+y2=25 （1）
| x2 |
| 45 |
| y2 |
| 20 |
由（1）（2）得：
x2=9，y2=9
解得：x1=-3，x2=3，y1=4，y2=-4，
椭圆
| x2 |
| 45 |
| y2 |
| 20 |
即椭圆与圆的交点，
所以交点坐标是（-3，-4），（-3，4），（3，-4），（3，4）．
点评：本题主要考查椭圆的性质，属于基础题．
练习册系列答案
相关题目
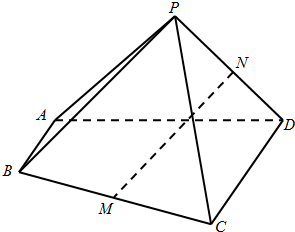如图，四棱锥P-ABCD中，AB∥CD，AB⊥AD，BC=CD=2AB=2，△PAD是等边三角形，M、N分别为BC、PD的中点．