题目内容
已知数列{an}中,a1=5,a2=2,且2(an+an+2)=5an+1.求证:
(1)数列{an+1-2an}和{an+1-
an}都是等比数列;
(2)求数列{2n-3an}的前n项和Sn.
(1)数列{an+1-2an}和{an+1-
| 1 |
| 2 |
(2)求数列{2n-3an}的前n项和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)2(an+an+2)=5an+1.求可得2(an+2-2an+1)=an+1-2an,an+2-
an+1=2(an+1-
an),根据等比数列的定义判定出数列都是等比数列;
(2)由(1)解的an,再求出2n-3an=
(2-22n-5),再求出前n项和.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)解的an,再求出2n-3an=
| 2 |
| 3 |
解答:
解:(1)∵2(an+an+2)=5an+1,
∴2an+2an+2=5an+1,
∴2(an+2-2an+1)=an+1-2an,
∴
=
,
∴a2-2a1=2-2×5=-8,
∴{an+1-2an}是以-8为首项,
为公比的等比数列;
∴an+1-2an=-8×(
)n-1①
∵2(an+an+2)=5an+1,
∴an+2-
an+1=2(an+1-
an)
∴
=2,
∴a2-
a1=2-
×5=-
,
∴{an+1-
an}是以-
为首项,2为公比的等比数列;
∴an+1-
an=-
×2n-1②,
(2)由(1)知an+1-2an=-8×(
)n-1①
an+1-
an=-
×2n-1②,
由①②解得
an=
(24-n-2n-2),
验证a1=5,a2=2适合上式,
∴2n-3an═
(24-n-2n-2)•2n-3=
(2-22n-5)
∴Sn=
(2-2-3)+
(2-2-1)+
(2-2)+…+
((2-22n-5)=
[2n-(2-3+2-1+2+…+22n-5)]=
[2n-
]=
+
-
∴2an+2an+2=5an+1,
∴2(an+2-2an+1)=an+1-2an,
∴
| an+2-2an+1 |
| an+1-2an |
| 1 |
| 2 |
∴a2-2a1=2-2×5=-8,
∴{an+1-2an}是以-8为首项,
| 1 |
| 2 |
∴an+1-2an=-8×(
| 1 |
| 2 |
∵2(an+an+2)=5an+1,
∴an+2-
| 1 |
| 2 |
| 1 |
| 2 |
∴
an+2-
| ||
an+1-
|
∴a2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴{an+1-
| 1 |
| 2 |
| 1 |
| 2 |
∴an+1-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知an+1-2an=-8×(
| 1 |
| 2 |
an+1-
| 1 |
| 2 |
| 1 |
| 2 |
由①②解得
an=
| 2 |
| 3 |
验证a1=5,a2=2适合上式,
∴2n-3an═
| 2 |
| 3 |
| 2 |
| 3 |
∴Sn=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 1-4 |
| 4n |
| 3 |
| 4n |
| 36 |
| 1 |
| 36 |
点评:本题主要考查了等比关系的确定,等比数列的求和问题.解题的关键是对等比数列基础知识点的熟练掌握,属于中档题

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
下列函数中,为奇函数的是( )
A、f(x)=
| ||
| B、f(x)=lnx | ||
| C、f(x)=2π | ||
| D、f(x)=sinx |
下列函数中,在区间(0,+∞)上为增函数的是( )
| A、y=log0.3(x+2) | ||
| B、y=3-x | ||
C、y=
| ||
| D、y=-x2 |
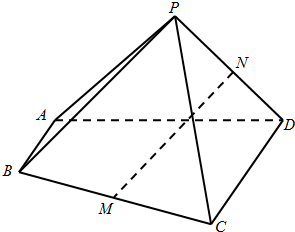 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.