题目内容
1.已知Sn为数列{an}的前n项和,若Sn=nan+1+2n,则数列{$\frac{1}{n({a}_{n}-{a}_{n+1})}$}的前n项和Tn=$\frac{3}{2}$-$\frac{2}{{2}^{n}}$.分析 Sn=nan+1+2n,a1=1,可得a1=a2+2,解得a2,当n≥2时,an=Sn-Sn-1,可得n(an-an+1)=2n-1;$\frac{1}{n({a}_{n}-{a}_{n+1})}$=$\frac{1}{{2}^{n-1}}$,T1=$\frac{1}{{a}_{1}-{a}_{2}}$=$\frac{1}{2}$.即可得出.
解答 解:∵Sn=nan+1+2n,a1=1,∴a1=a2+2,解得a2=-1,
当n≥2时,an=Sn-Sn-1=nan+1+2n-(n-1)an-2n-1,∴n(an-an+1)=2n-1;
∴$\frac{1}{n({a}_{n}-{a}_{n+1})}$=$\frac{1}{{2}^{n-1}}$,T1=$\frac{1}{{a}_{1}-{a}_{2}}$=$\frac{1}{2}$.
数列{$\frac{1}{n({a}_{n}-{a}_{n+1})}$}的前n项和Tn=$\frac{1}{2}$+$\frac{1}{2}+\frac{1}{{2}^{2}}$+…$\frac{1}{{2}^{n-1}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{1}{2}$=$\frac{3}{2}$-$\frac{2}{{2}^{n}}$.
故答案为:$\frac{3}{2}$-$\frac{2}{{2}^{n}}$.
点评 本题考查了等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
9.已知集合M={x|-1≤x≤1},N={x|y=$\sqrt{x}$+ln(1-x)},则M∩N=( )
| A. | [0,1) | B. | (0,1) | C. | [0,+∞) | D. | (0,1] |
16.在△ABC中,角A,B,C的对边分别为a,b,c,满足asinA-csinC=(a-b)sinB,则角C的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
6.已知集合M={y|y=2x,x>0},N={x|y=lgx},则M∩N为( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,+∞) |
10.已知$\frac{(1-i)^{2}}{z}$=1+i(i为虚数单位),则复数z的虚部为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
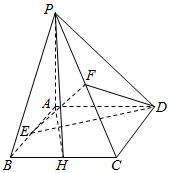 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点