题目内容
11.已知{an}为等比数列,下列结论①a3+a5≥2a4;
②$a_3^2+a_5^2≥2a_4^2$;
③若a3=a5,则a1=a2;
④若a5>a3,则a7>a5.
其中正确结论的序号是②④.
分析 根据等比数列的性质结合不等式的关系进行判断即可.
解答 解:①an=(-1)n,则a3+a5≥2a4不成立,故①错误,
②∵a32+a52≥2|a3a5|=2a42;故$a_3^2+a_5^2≥2a_4^2$;故②正确,
③若an=(-1)n,则a3=a5=-1,但a1=-1,a2=1,a1=a2;不成立,故③错误,
④若a5>a3,则q2a3>a3,∵q2>0,
∴q2a5>q2a3,即a7>a5成立,故④正确,
故正确的是②④,
故答案为:②④.
点评 本题主要考查与等比数列有关的命题的真假判断,利用等比数列的性质,结合不等式的性质是解决本题的关键.

练习册系列答案
相关题目
2.已知二次函数f(x)=ax2+bx(|b|≤2|a|),定义f1(x)=max{f(t)|-1≤t≤x≤1},f2(x)=min{f(t)|-1≤t≤x≤1},其中max{a,b}表示a,b中的较大者,min{a,b}表示a,b中的较小者,则下列命题正确的是( )
| A. | 若f1(-1)=f1(1),则f(-1)>f(1) | B. | 若f2(-1)=f2(1),则f(-1)>f(1) | ||
| C. | 若f(-1)=f(1),则f2(-1)>f2(1) | D. | 若f2(1)=f1(-1),则f1(-1)<f1(1) |
6.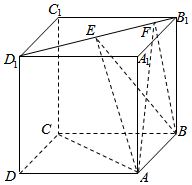 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )| A. | AC⊥BF | B. | 三棱锥A-BEF的体积为定值 | ||
| C. | EF∥平面ABCD | D. | 面直线AE、BF所成的角为定值 |
3.设函数$f(x)=\left\{\begin{array}{l}{x^2}-6x+6,x≥0\\ 3x+4,x<0\end{array}\right.$,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
| A. | $({\frac{11}{6},6}]$ | B. | $({\frac{11}{3},6})$ | C. | $({\frac{20}{3},\frac{26}{3}})$ | D. | $({\frac{20}{3},\frac{26}{3}}]$ |
20.运行如图所示的程序框图,若输出的点恰有5次落在直线y=x上,则判断框中可填写的条件是( )


| A. | i>6 | B. | i>7 | C. | i>8 | D. | i>9 |
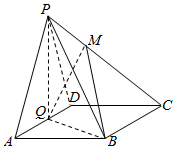 如图,在四棱锥P-ABCD中,底面ABCD为棱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为棱形,∠BAD=60°,Q为AD的中点.