题目内容
13.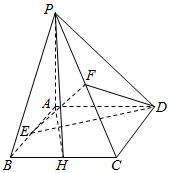 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:平面PAH⊥平面DEF.
分析 (Ⅰ)取CD中点N,连接FN,EN,则FN∥PD,EN∥AD,故而平面EFN∥平面PAD,所以EF∥平面PAD;
(Ⅱ)由侧面PAD⊥底面ABCD可得PA⊥平面ABCD,故PA⊥DE,由正方形的性质可得DE⊥AH,故DE⊥平面PAH,于是平面PAH⊥平面DEF.
解答  证明:(Ⅰ)取CD中点N,连接FN,EN.
证明:(Ⅰ)取CD中点N,连接FN,EN.
∵在△CPD中,F,N为中点,∴FN∥PD.
∵正方形ABCD中,E,N为中点,
∴EN∥AD,
∵EN?平面EFN,FN?平面EFN,EN∩FN=N,PD?平面PAD,AD?平面PAD,PD∩AD=D,
∴平面EFN∥平面PAD,∵EF?平面EFN,
∴EF∥平面PAD.
(Ⅱ)∵侧面PAD⊥底面ABCD,PA⊥AD,侧面PAD∩底面ABCD=AD,
∴PA⊥底面ABCD,∵DE?底面ABCD,
∴DE⊥PA,
∵E,H分别为正方形ABCD边AB,BC中点,
∴Rt△ABH≌Rt△ADE,则∠BAH=∠ADE,∴∠BAH+∠AED=90°,则DE⊥AH,
∵PA?平面PAH,AH?平面PAH,PA∩AH=A,
∴DE⊥平面PAH,∵DE?平面EFD,
∴平面PAH⊥平面DEF.
点评 本题考查了线面平行,面面垂直的性质与判定,属于中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
3.设函数$f(x)=\left\{\begin{array}{l}{x^2}-6x+6,x≥0\\ 3x+4,x<0\end{array}\right.$,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
| A. | $({\frac{11}{6},6}]$ | B. | $({\frac{11}{3},6})$ | C. | $({\frac{20}{3},\frac{26}{3}})$ | D. | $({\frac{20}{3},\frac{26}{3}}]$ |
 已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.