题目内容
16．三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为3的正三角形，SC是球O的直径，且SC=4，则此三棱锥的体积V=$\frac{3\sqrt{3}}{2}$．分析 根据题意，利用截面圆的性质即可求出点O到平面ABC的距离，进而求出点S到平面ABC的距离，即可计算出三棱锥的体积．
解答 解：因为△ABC是边长为3的正三角形，所以△ABC外接圆的半径r=$\sqrt{3}$，
所以点O到平面ABC的距离d=$\sqrt{{R}^{2}-{r}^{2}}=1$，
SC为球O的直径，点S到平面ABC的距离为2d=2，
此棱锥的体积为V=$\frac{1}{3}{s}_{ABC}×2d$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{3}^{2}×2=\frac{3\sqrt{3}}{2}$，
故答案为：$\frac{{3\sqrt{3}}}{2}$．
点评 题考查三棱锥的体积，考查学生的计算能力，求出点O到平面ABC的距离，进而求出点S到平面ABC的距离是关键，属于中档题．
练习册系列答案
相关题目
6．函数y=2sin2x的最小正周期为（ ）
| A． | 4π | B． | 3π | C． | 2π | D． | π |
7．已知a，b，c分别为△ABC三个内角A，B，C的对边，a=2，且（2+b）（sinA-sinB）=（c-b）sinC，则A的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
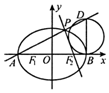已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{1}{2}$，左、右焦点为F1，F2，点M为椭圆C上的任意一点，$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2．