题目内容
已知x∈[0,4],则满足不等式log
(x-1)>0的概率为 .
| 1 |
| 2 |
考点:几何概型
专题:计算题,概率与统计
分析:解不等式式log
(x-1)>0,可得1<x<
,以长度为测度,即可求在区间[0,4]上随机取一实数x,该实数x满足不等式式log
(x-1)>0的概率.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:本题属于几何概型
解不等式式log
(x-1)>0,可得1<x<
,
∴在区间[0,4]上随机取一实数x,该实数x满足不等式式log
(x-1)>0的概率为
=
.
故答案为:
.
解不等式式log
| 1 |
| 2 |
| 3 |
| 2 |
∴在区间[0,4]上随机取一实数x,该实数x满足不等式式log
| 1 |
| 2 |
| ||
| 4-0 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题考查几何概型,解题的关键是解不等式,确定其测度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
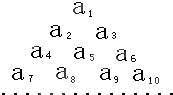 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=