题目内容
已知某几何体的三视图（单位：cm）如图所示，则该几何体的表面积是（ ）| A、1cm2 | ||||
| B、3cm2 | ||||
C、（2
| ||||
D、（
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知：该几何体是以俯视图为底面的三棱锥，计算出几何体的底面面积和高，代入棱锥体积公式，可得答案．
解答：
解：由已知中的三视图可知：该几何体是以俯视图为底面的三棱锥，
其直观图如下图所示：
其底面面积S△ABC=
×22=
，
侧面积面积S△PAC=
×2×
=
，
侧面积面积S△PAB=S△PBC=
×
×
=
，
故棱锥的表面积S=S△ABC+S△PAC+S△PAB+S△PBC=2
+
故选：C
其直观图如下图所示：
其底面面积S△ABC=
| ||
| 4 |
| 3 |
侧面积面积S△PAC=
| 1 |
| 2 |
| 3 |
| 3 |
侧面积面积S△PAB=S△PBC=
| 1 |
| 2 |
| 6 |
| ||
| 2 |
| ||
| 2 |
故棱锥的表面积S=S△ABC+S△PAC+S△PAB+S△PBC=2
| 3 |
| 15 |
故选：C
点评：本题考查的知识点是由三视图求表面积，其中分析出几何体的形状是解答的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
设a=（
） log23，b=（
） log54，c=3ln3，则a，b，c的大小关系是（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| A、c＞a＞b |
| B、c＞b＞a |
| C、a＞b＞c |
| D、a＞c＞b |
在△ABC中，AB=AC=2，BC=2
，则
•
=（ ）
| 3 |
| AB |
| AC |
A、2
| ||
| B、2 | ||
C、-2
| ||
| D、-2 |
下面是一个2×2列联表：
则表中a，b的值分别为（ ）
| y1 | y2 | 合计 | |
| x1 | a | c | 73 |
| x2 | 22 | 25 | 47 |
| 合计 | b | 46 | 120 |
| A、94，72 |
| B、52，50 |
| C、52，74 |
| D、74，52 |
已知函数f（x）=
，则f（f（-
））的值为（ ）
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
质点做直线运动，其速度v（t）=3t2-2t+3，则它在第2秒内所走的路程为（ ）
| A、1 | B、3 | C、5 | D、7 |
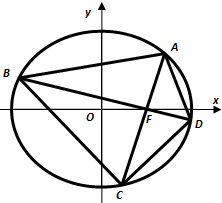已知椭圆Γ：